Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://hoc24.vn/cau-hoi/cho-goc-nhon-xoy-lay-diem-ab-thuoc-tia-ox-sao-cho-oa-ob-lay-diem-cd-thuoc-tia-oy-sao-cho-oaob-lay-diem-c-d-thuoc-tia-oy-sao-cho-ocoa-od.7621651044223
có ng trả lời cho bn rùi mà

a: Xét ΔOAD và ΔOCB có
OA=OC
góc AOD chung
OD=OB
=>ΔOAD=ΔOCB
=>AD=CB
b: Xét ΔEAB và ΔECD có
góc EAB=góc ECD
AB=CD
góc EBA=góc EDC
=>ΔEAB=ΔECD
c: Xét ΔOAE và ΔOCE có
OA=OC
AE=CE
OE chung
=>ΔOAE=ΔOCE
=>góc AOE=góc COE
=>góc AOM=góc CON
Xét ΔCON và ΔAOM có
góc CON=góc AOM
CO=AO
góc OCN=góc OAM
=>ΔCON=ΔAOM
=>ON=OM
=>ΔENM can tại E
=>EM=EN
=>NC=MA
Xét ΔEMB và ΔEND có
EM=EN
góc MEB=góc NED
EB=ED
=>ΔEMB=ΔEND
=>ND=MB và góc EMB=góc END
=>góc KMO=góc KNO
=>ΔKMN cân tại K
KD+DN=KN
KB+BM=KM
mà KM=KN; DN=BM
nên KD=KB
=>K nằm trên trung trực của DB(1)
OB=OD
nên O nằm trên trung trực của DB(2)
EB=ED
nên E nằm trên trung trực của DB(3)
Từ (1), (2), (3) suy ra O,E,K thẳng hàng

Tham khảo:
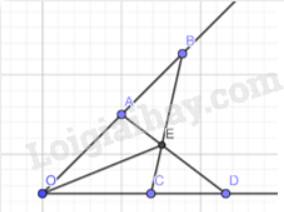
a) Xét \(\Delta OAD\) và \(\Delta OCB\), ta có :
OD = OB
\(\widehat{A}\) chung
OA = OC
\(\Rightarrow \Delta OAD=\Delta OCB\) (c-g-c )
\( \Rightarrow AD = BC\)(2 cạnh tương ứng )
b) Vì \(\Delta OAD=\Delta OCB\) nên \(\widehat{OAD}=\widehat{OCB}; \widehat{D}=\widehat{B}\) ( 2 góc tương ứng)
Mà \(\widehat{OAD}+\widehat{BAD}=180^0\) ( 2 góc kề bù)
\(\widehat{OCB}+\widehat{BCD}=180^0\) ( 2 góc kề bù)
Do đó, \(\widehat{BAD}=\widehat{BCD}\)
Vì \(OA+AB=OB; OC+CD=OD\)
Mà \(OC = OA, OD = OB\)
\(\Rightarrow AB=CD\)
Xét \(\Delta EAB\) và \(\Delta ECD\), ta có:
\(\widehat {ABE} = \widehat {CDE}\)
\(AB = CD\)
\(\widehat {BAE} = \widehat {DCE}\)
\(\Rightarrow \Delta EAB=\Delta ECD\) (g-c-g)
c) Vì \(\Delta EAB=\Delta ECD\) nên EB = ED ( 2 cạnh tương ứng)
Xét \(\Delta OBE\) và \(\Delta ODE\), ta có :
EB = ED
OB = OD
OE chung
\( \Rightarrow \Delta OBE=\Delta ODE \) (c.c.c)
\( \Rightarrow \widehat{BOE}=\widehat{DOE}\) ( 2 góc tương ứng)
\( \Rightarrow \) OE là phân giác \(\widehat {xOy}\)

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy

a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
\(a,\left\{{}\begin{matrix}OA=OC\\OD=OB\\\widehat{AOB}\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOD=\Delta COB\left(c.g.c\right)\\ \Rightarrow AD=BC\\ b,\Delta AOD=\Delta COB\\ \Rightarrow\widehat{ADO}=\widehat{CBO};\widehat{OAD}=\widehat{OCB}\\ \Rightarrow180^0-\widehat{OAD}=180^0-\widehat{OCB}\\ \Rightarrow\widehat{ECD}=\widehat{EAB}\\ \text{Ta có}\left\{{}\begin{matrix}OA=OC\\OD=OB\end{matrix}\right.\Rightarrow CD=OD-OC=OB-OA=AB\\ \left\{{}\begin{matrix}AB=CD\\\widehat{ADO}=\widehat{CBO}\\\widehat{ECD}=\widehat{EAB}\end{matrix}\right.\Rightarrow\Delta EAB=\Delta ECD\left(g.c.g\right)\)

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
a: Xet ΔOAD và ΔOCB có
OA=OC
góc O chung
OD=OB
=>ΔOAD=ΔOCB
=>AD=CB
b: Xét ΔEAB và ΔECD có
góc EAB=góc ECD
AB=CD
góc EBA=góc EDC
=>ΔEAB=ΔECD
ý c đâu ạ