Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: Tiêu cự 2c= 6 => c= 3
Khoảng cách giữa 2 đường chuẩn .
2 a e = 50 3
=> 6a2= 50 c nên a2= 25 => b2= 16
Vậy phương trình (E) cần tìm là:
![]()
Chọn C.

a) Từ phương trình tổng quát của đường thẳng, ta lấy được một vecto pháp tuyến là: \(\overrightarrow n = \left( {1; - 2} \right)\) nên ta chọn vecto chỉ phương của đường thẳng d là: \(\overrightarrow u = \left( {2;1} \right)\).
Chọn điểm \(A\left( {1; - 2} \right) \in d\).Vậy phương trình tham số của đường thẳng d là: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\end{array} \right.\) (t là tham số)
b) Do điểm M thuộc d nên ta có: \(M\left( {1 + 2m; - 2 + m} \right);m \in \mathbb{R}\).
Ta có: \(OM = 5 \Leftrightarrow \sqrt {{{\left( {1 + 2m} \right)}^2} + {{\left( { - 2 + m} \right)}^2}} = 5 \Leftrightarrow {m^2} = 4 \Leftrightarrow m = \pm 2\)
Với \(m = 2 \Rightarrow M\left( {5;0} \right)\)
Với \(m = - 2 \Rightarrow M\left( { - 3; - 4} \right)\)
Vậy ta có 2 điểm M thỏa mãn điều kiện đề bài.
c) Do điểm N thuộc d nên ta có: \(N\left( {1 + 2n; - 2 + n} \right)\)
Khoảng cách từ N đến trục hoành bằng giá trị tuyệt đối của tung độ điểm N. Do đó, khoảng cách tư N đến trục hoành bằng 3 khi và chỉ khi: \(\left| { - 2 + n} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}n = 5\\n = - 1\end{array} \right.\)
Với \(n = 5 \Rightarrow N\left( {11;3} \right)\)
Với \(n = - 1 \Rightarrow N\left( { - 1; - 3} \right)\)
Vậy có 2 điểm N thỏa mãn bài toán

Đáp án A
- A: B có hoành độ là hoành độ của 2 đỉnh của 2 bán trục lớn của (E) , chúng nằm trên đường thẳng y+ 2= 0. Điểm C có hoành độ và tung độ dương thì C nằm trên cung phần tư thứ nhất
- Tam giác ABC có AB= 6 cố định. Vì thế tam giác có diện tích lớn nhất khi khoảng cách từ C đến AB lớn nhất.
- Dễ nhận thấy C trùng với đỉnh của bán trục lớn (0; 3).

a: Phương trình tổng quát là:
3(x-1)+1(y+3)=0
=>3x-3+y+3=0
=>3x+y=0
b: vecto AB=(-1;4)
Phương trình tham số của AB là:
\(\left\{{}\begin{matrix}x=1-t\\y=-3+4t\end{matrix}\right.\)
c: \(d\left(B;d\right)=\dfrac{\left|0\cdot3+1\cdot1\right|}{\sqrt{3^2+1^2}}=\dfrac{1}{\sqrt{10}}\)

a: Tọa độ trọng tâm là:
x=(1+2+0)/3=1 và y=(3+1+3)/3=7/3
c: \(d\left(A;d\right)=\dfrac{\left|1\cdot1+3\cdot\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\sqrt{2}}{2}\)
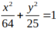
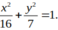
Ta có:
Tổng khoảng cách từ 1 điểm thuộc Elip đến 2 tiêu điểm bẳng 2a= 5.
Chọn C.