Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

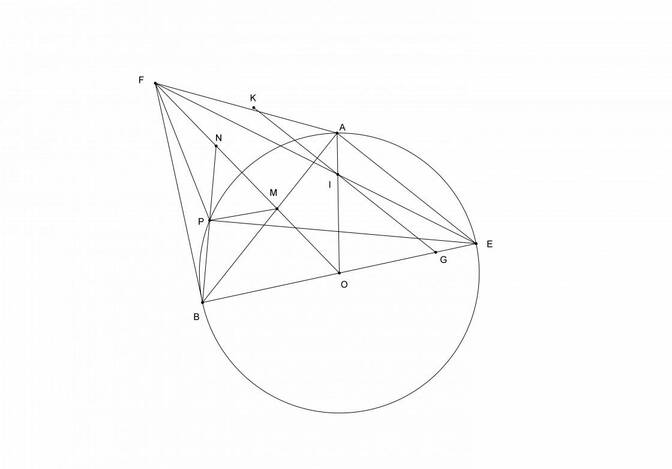
a. Tứ giác AOBF nội tiếp vì có $\angle OAF=\angle OBF=90^o$
b. Chú ý rằng $OF\perp AB$ nên $OF\parallel AE$, ta biến đổi tỉ số bằng định lý Thales:
\(\dfrac{IK}{OF}=\dfrac{AK}{AF}=\dfrac{EG}{EO}=\dfrac{IG}{OF}\), vậy $IK=IG$
c. Nếu mình không nhầm thì PM không vuông NB, vì khi đó $M,P,E$ thẳng hàng, bạn có thể kiểm tra hình vẽ của mình :c

a/
Ta có A và B cùng nhìn FO dưới 1 góc vuông => A và B thuộc đường tròn đường kính FO
=> AOBF là tứ giác nội tiếp
b/
Ta có
\(\widehat{BAE}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow AE\perp AB\) (1)
\(FO\perp AB\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm đường tròn vuông góc và chia đôi dây cung nối 2 tiếp điểm) (2)
Từ (1) và (2) => AE//FO mà KG//AE (gt) => AE//KG//FO
\(\Rightarrow\dfrac{FK}{FA}=\dfrac{OG}{OE}\) (Talet) (1)
Xét tg AFE có
\(\dfrac{FK}{FA}=\dfrac{IK}{AE}\) (Talet trong tam giác) (2)
Xét tg OAE có
\(\dfrac{OG}{OE}=\dfrac{IG}{AE}\) (Talet trong tam giác) (3)
Từ (1) (2) (3) \(\Rightarrow\dfrac{IK}{AE}=\dfrac{IG}{AE}\Rightarrow IK=IG\)
c/ Câu này mình nghĩ bạn nên kiểm tra lại đề bài

Hình tự vẽ nha e
a) Xét (O) có EF là dây cung, I là trung điểm của EF
=> OI vuông góc với EF (tính chất đường kính và dây)
=> \(\widehat{OIA}=90^o\)
Lại có : (O) có AB là tiếp tuyến tại B
=> AB vuông góc với OB (tc tiếp tuyến)
=> \(\widehat{ABO}=90^o\)
Xét tứ giác ABOI có \(\widehat{ABO}+\widehat{OIA}=90+90=180^o\) mà 2 góc này là 2 góc đối của tứ giác
=> tứ giác ABOI nt đường tròn (ĐPCM)
b) ta có tứ giác ABOI nt
=> \(\widehat{OAI}=\widehat{OBI}\)(2 góc nt cùng chắn cung OI)
mà \(\widehat{OAI}=\widehat{DIF}\)(2 góc so le trong, AO//FK)
=> \(\widehat{KBI}=\widehat{IFK}\)
Xét tứ giác BIKF có \(\widehat{KBI}=\widehat{IFK}\)
mà 2 góc trên là góc nội tiếp cùng chằn cung CI
=> tứ giác BIKF nt hay 4 điểm B,I,K,F cùng thuộc 1 đg tròn
chúc e học tốt
sao IFK chắn cung IC đk anh