Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔOBA vuông tại B có sin BAO=OB/OA=1/2
nên góc BAO=30 độ
Xét ΔOBI có OB=OI và góc BOI=60 độ
nên ΔOBI đều
=>OI=OB=1/2OA
=>AI*AO=2R^2
Xét ΔBDE vuông tại D có DC vuông góc BE
nên ΔBDE vuông tại D
=>BC*BE=BD^2=4R^2
=>BC*BE+AI*AO=6R^2

Ta có
\(AB=AC\) (Hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến hai tiếp điểm bằng nhau)
\(\Rightarrow\Delta ABC\) cân tại A (1)
AO là phân giác của \(\widehat{BAC}\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm của đường tròn là phân iacs của góc tạo bởi 2 tiếp tuyến) (2)
Từ (1) và (2) \(\Rightarrow AH\perp BC\) (Trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AHE}=90^o\) (*)
Ta có
\(OM=ON\) (Bán kính (O)) \(\Rightarrow\Delta OMN\) cân tại O
Ta có \(IM=IN\) (Giả thiết) => ON là đường trung tuyến của tg OMN
\(\Rightarrow OE\perp AN\) (Trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AIE}=90^o\) (**)
Từ (*) và (**) => I và H cùng nhìn AE dưới hai góc bằng nhau và bằng 90 độ => I và H nằm trên đường tròn đường kính AE nên 4 điểm A;H;I;E cùng nằm trên 1 đường tròn
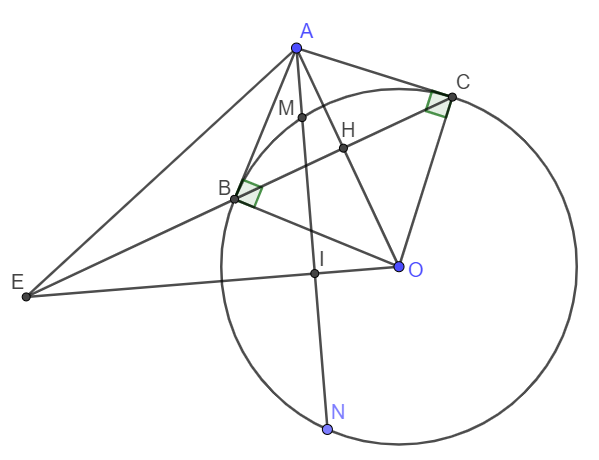
Cho đường tròn tâm bán kính và một điểm nằm ngoài đường tròn. Kẻ một đường thẳng đi qua và không đi qua , cắt đường tròn tại hai điểm phân biệt , ( nằm giữa và ). Từ vẽ hai tiếp tuyến và với (, là hai tiếp điểm). Đường thẳng cắt tại . Gọi là trung điểm của . Đường thẳng cắt đường thẳng tại . Chứng minh là tứ giác nội tiếp.
theo gt, ta co:
là trung điểm của

Câu c.
Gọi K là trung điểm của BH
Chỉ ra K là trực tâm của tam giác BMI
Chứng minh MK//EI
Chứng minh M là trung điểm của BE (t.c đường trung bình)

Tam giác CDK đồng dạng Tam giác ABO ( g.g) => CK/BA = DK/OB => CK.OB=BA.DK (1) . Tam giác DBA có IK//BA => IK/BA = DK/BD => IK.BD=BA.DK (2) . Từ (1) (2) =>CK.OB=IK.BD => CK.OB=IK.2OB=> CK=2IK . Lập luận 1 tí rồi suy ra điều phải chứng minh
a) Ta thấy: Đường tròn (O) có đường kính CD và điểm M thuộc cung CD => ^CMD = 900 => ^CMA = 900.
Đường tròn (O) có 2 tiếp tuyến AB và AC => AB=AC => \(\Delta\)ABC cân tại A
Mà AO là phân giác ^BAC (T/c 2 tiếp tuyến cắt nhau) => AO vuông góc BC hay AH vuông góc BC
=> ^AHC = 900
Xét tứ giác AMHC: ^AHC = ^CMA = 900 => Tứ giác AMHC nội tiếp đường tròn (đpcm).
b) Tứ giác AMHC nội tiếp đường tròn => ^AHM = ^ACM (Cùng chắn cung AM)
Xét \(\Delta\)ACD: ^ACD = 900; CM vuông góc AD => ^ACM = ^CDM
=> ^AHM = ^CDM (1)
Dễ thấy tứ giác BDCM nội tiếp (O) => ^CDM = ^CBM (2)
Từ (1) và (2) => ^AHM = ^CBM hay ^NHM = ^HBM
Mà ^NHM + ^BHM = 900 nên ^HBM + ^BHM = 900 => \(\Delta\)BMH vuông đỉnh M
=> ^HMN = 900 => ^HMC = ^NMA (Cùng phụ ^CMN)
Xét \(\Delta\)MHC và \(\Delta\)MNA: ^HMC = ^NMA (cmt); ^HCM = ^NAM (Do tứ giác AMHC nột tiếp)
=> \(\Delta\)MHC ~ \(\Delta\)MNA (g.g) => \(\frac{HC}{NA}=\frac{MH}{MN}\)hay \(\frac{NA}{HC}=\frac{MN}{MH}\)(3)
Dễ chứng minh: \(\Delta\)HMN ~ \(\Delta\)BMH (g.g) => \(\frac{HN}{BH}=\frac{MN}{HM}\)(4)
Từ (3) và (4) => \(\frac{NA}{HC}=\frac{HN}{BH}\).
Lại có: \(\Delta\)ABC cân tại A có đường cao AH => AH là đường trung tuyến => HC=BH
Từ đó suy ra: NA = HN => N là trung điểm của AH (đpcm).
Em cảm ơn nhiều ạ.<3