Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại B và ΔDBE vuông tại B có
BE chung
BA=BD
=>ΔABE=ΔDBE
=>EA=ED
=>ΔEAD cân tại E
Xét ΔKBA vuông tại K và ΔFBD vuông tại F có
BA=BD
góc KBA=góc FBD
=>ΔKBA=ΔFBD
=>BK=BF
=>B là trung điểm của KF

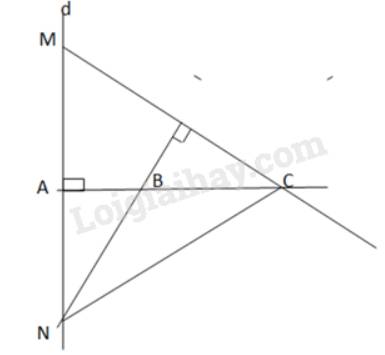
Xét tam giác MNC có 2 đường cao CA và NB cắt nhau tại B
\( \Rightarrow \) B là trực tâm của tam giác MNC
\( \Rightarrow MB \bot CN\)

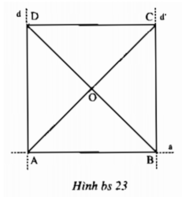
Gọi giao điểm của đg thẳng vuông góc với AD cắt AD tại T
Xét tam giác ANC vuông tại C và tam giác ANT vuông tại T có
AN^2=AT^2 + TN^2 (Đlí Py-ta-go)
AN^2=CN^2 + AC^2
=> AT^2+TN^2=CN^2+AC^2 (1)
Xét tam giác TND vuông tại T, tam giác KDT vuông tại T, tam giác ATK vuông tại T, tam giác ABK vuông tại B có
ND^2=TD^2+TN^2
KD^2=TD^2+TK^2
AK^2=AT^2+TK^2
AK^2=AB^2+BK^2
=>(1) <=> AC^2 + NC^2-NT^2 =AT^2
Mà NC=ND( Vì N là trung điểm của CD ) ;AB=AC (GT)
=> AC^2+NC^2-NT^2=AT^2 <=> AC^2 + ND^2 - NT^2 = AT^2
<=> AC^2 + (ND^2 - NT^2)= AT^2
<=>AB^2 + TD^2 = AT^2
<=> AB^2+(KD^2 - KT^2) = AT^2
<=> AB^2 + KD^2 - KT^2 =AT^2
<=> KD^2 - ( KT^2 + AT^2)= -(AB)^2
<=> KD^2 - AK^2 = -(AB)^2
<=> KD^2 = AK^2 - AB^2
<=> KD^2 = BK^2
<=> KD = KB
Vậy KB = KD
Gọi giao điểm của dường thẳng vuông góc với AD cắt AD tại T
Xét tam giác ANC vuông tại C và tam giác ANT vuông tại T , ta có :
\(AN^2=AT^2+TN^2\)( định lí Py-ta-go )
\(AN^2=CN^2+AC^2\)
\(\Rightarrow AT^2+TN^2=CN^2+AC^2\left(1\right)\)
Xét tam giác TND vuông tại T , KDT vuông tại T , ATK vuông tại T , ABK vuông tại B : Ta có :
\(ND^2=TD^2+TN^2\)
\(KD^2=TD^2+TK^2\)
\(AK^2=AT^2+TK^2\)
\(AK^2=AB^2+BK^2\)
\(\Rightarrow\left(1\right)\Leftrightarrow AC^2+NC^2-NT^2=AT^2\)
Mà NC = ND ( Vì N là trung điểm của CD )
AB = AC(gt)
\(\Rightarrow AC^2+NC^2-NT^2=AT^2\Leftrightarrow AC^2+ND^2-NT^2=AT^2\)
\(\Leftrightarrow AC^2+\left(ND^2-NT^2\right)=AT^2\)
\(\Leftrightarrow AB^2+TD^2=AT^2\)
\(\Leftrightarrow AB^2+\left(KD^2-KT^2\right)=AT^2\)
\(\Leftrightarrow AB^2+KD^2-KT^2=AT^2\)
Bạn tự làm tiếp nhé~