Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(\frac{1}{R_{234}}=\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}=\frac{1}{10}+\frac{1}{6}+\frac{1}{9}=\frac{17}{45}\)
\(\Leftrightarrow R_{234}=\frac{45}{17}\left(Ôm\right)\)
\(R_m=R_1+R_{234}=5+\frac{45}{17}=\frac{130}{17}\left(Ôm\right)\)
b/ \(I_m=\frac{U}{R_m}=\frac{15}{\frac{130}{17}}=\frac{51}{26}\left(A\right)=I_1=I_{234}\)
\(U_{234}=I_{234}.R_{234}=\frac{51}{26}.\frac{45}{17}=\frac{135}{26}\left(V\right)=U_2=U_3=U_4\)
\(I_2=\frac{U_2}{R_2}=\frac{\frac{135}{26}}{10}=\frac{27}{52}\left(A\right)\)
\(I_3=\frac{U_3}{R_3}=\frac{\frac{135}{26}}{6}=\frac{45}{52}\left(A\right)\)
\(I_4=\frac{U_4}{R_4}=\frac{\frac{135}{26}}{9}=\frac{15}{26}\left(A\right)\)
Vậy...

a)Ta có (R1//R3)nt(R2//R4)=> Rtđ=R13+R24=\(\dfrac{R1.R3}{R1+R3}+\dfrac{R2.R4}{R2+R4}=1+2=3\Omega\)
=> I=\(\dfrac{U}{Rt\text{đ}}=\dfrac{5}{3}A\)
Vì R13ntR24=>I13=I24=I=\(\dfrac{5}{3}A\)
Vì R1//R3=> U1=U3=U13=I13.R13=\(\dfrac{5}{3}.1=\dfrac{5}{3}V\)
=> I1=\(\dfrac{U1}{R1}=\dfrac{5}{3}:2=\dfrac{5}{6}A;I3=\dfrac{U3}{R3}=\dfrac{5}{3}:2=\dfrac{5}{6}A\)
Vì R2//R4=> U2=U4=U24=I24.R24=\(\dfrac{5}{3}.2=\dfrac{10}{3}V\)
=> I2=\(\dfrac{U2}{R2}=\dfrac{10}{3}:3=\dfrac{10}{9}A;I4=\dfrac{U4}{R4}=\dfrac{10}{3}:6=\dfrac{5}{9}A\)
Vì I1<I2=> Chốt dương tại D
=> I1+Ia=I2=> Ia=I2-I1=\(\dfrac{5}{18}A\)
Vậy ampe kế chỉ 5/18 A

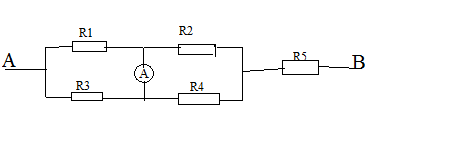
a, \(=>R5nt\left[\left(R1//R3\right)nt\left(R2//R4\right)\right]\)
\(=>Rtd=R5+\dfrac{R1R3}{R1+R3}+\dfrac{R2.R4}{R2+R4}=1,2+\dfrac{8.12}{8+12}+\dfrac{8.24}{8+24}\)\(=12\left(om\right)\)
b,\(=>Im=\dfrac{4}{12}=\dfrac{1}{3}A=I5=I13=I24\)
\(=>U13=\dfrac{1}{3}\left(\dfrac{8.12}{8+12}\right)=1,6V=U1=U3\)
\(=>I1=\dfrac{1,6}{8}=0,2A,I3=\dfrac{1,6}{12}=\dfrac{2}{15}A\)
\(=>U24=\dfrac{1}{3}\left(\dfrac{8,24}{8+24}\right)=2V=U2=U4\)
\(=>I2=\dfrac{2}{8}=0,25A,I4=\dfrac{2}{24}=\dfrac{1}{12}A\)
c, giả sử chiều dòng điện qua ampe kế từ M đến N
\(=>I1=Ia+I2=>Ia=I1-I2=0,2-0,25=-0,05A\)
=>chiều dòng điện phải từ N tới M =>số chỉ ampe kế là 0,05A

ý là thế này hả bn?
(R1ntR2)//(R3ntR4)
a,\(=>Rtd=\dfrac{\left(R1+R2\right)\left(R3+R4\right)}{R1+R2+R3+R4}=\dfrac{\left(10+15\right)\left(10+25\right)}{10+15+10+25}=\dfrac{175}{12}\left(om\right)\)
b,\(=>U12=U34=36V\)
\(=>I12=I1=I2=\dfrac{U12}{R12}=\dfrac{36}{10+15}=1,44A\)
\(=>I34=I3=I4=\dfrac{U34}{R34}=\dfrac{36}{10+25}=\dfrac{36}{35}A\)

\(R_{12}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{12\cdot6}{12+6}=4\Omega\)
\(R_{34}=R_{tđ}-R_{12}=10-4=6\Omega\)
\(\dfrac{1}{R_{34}}=\dfrac{1}{R_3}+\dfrac{1}{R_4}=\dfrac{1}{24}+\dfrac{1}{R_4}=\dfrac{1}{6}\)
\(\Rightarrow R_4=8\Omega\)

Bài dễ mà bn, ADCT là ra :))
Có \(R_{tđ}=\frac{R_1.R_2}{R_1+R_2}+\frac{R_3.R_4}{R_3+R_4}=\frac{30.60}{30+60}+\frac{60.R_3}{60+R_3}\)\(=20+\frac{60.R_3}{60+R_3}\)
Có \(R_{tđ}=\frac{U_{AB}}{I}=\frac{22}{0,5}=44\left(\Omega\right)\)
\(\Rightarrow20+\frac{60R_3}{60+R_3}=44\Leftrightarrow\frac{60R_3}{60+R_3}=24\)
\(\Leftrightarrow R_3=40\left(\Omega\right)\)
b/ Có I=I12=I34= 0,5(A)
\(\Rightarrow U_1=U_2=U_{12}=I_{12}.R_{12}=0,5.20=10\left(V\right)\)
\(\Rightarrow I_1=\frac{U_1}{R_1}=\frac{10}{30}=\frac{1}{3}\left(A\right)\)
\(\Rightarrow I_2=0,5-\frac{1}{3}=\frac{1}{6}\left(A\right)\)
\(\Rightarrow U_3=U_4=U_{34}=I_{34}.R_{34}=0,5.24=12\left(V\right)\)
\(\Rightarrow I_3=\frac{U_3}{R_3}=\frac{12}{40}=0,3\left(A\right)\)
\(\Rightarrow I_4=\frac{U_4}{R_4}=\frac{12}{60}=0,2\left(A\right)\)