Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Kẻ OF//BC(F thuộc AC)
=>OF//DE//BC
DE//BC
=>góc DEA=góc ACB
=>góc DEO=1/2*góc ACB
ED//OF
=>góc DEA=góc CFD và góc DEO=góc EOF
=>góc EOF=1/2*góc ACB
=>góc DEO=góc EOF
OF//BC
=>góc FOB=góc OBC=1/2góc ABC
góc BOE=góc BOF+góc EOF
=1/2(góc ABC+góc ACB)

Hình bạn tự vẽ.
Đây là lời giải của mình :
Trước hết biết được góc A thì tính được \(\widehat{ABC}+\widehat{ACB}=180^o-\widehat{A}=80^o\)
\(\widehat{ACx}=\widehat{A}+\widehat{ABC}=100^o+\widehat{ABC}\) ( góc ngoài tam giác )
\(\Rightarrow\frac{\widehat{ACx}}{2}=\widehat{ACN}=50^o+\frac{\widehat{ABC}}{2}\)
Do đó \(\widehat{BCN}=\widehat{ACB}+\widehat{ACN}=50^o+\frac{\widehat{ABC}}{2}+\widehat{ACB}\)
BI là phân giác góc ABC nên \(\widehat{NBC}=\frac{\widehat{ABC}}{2}\)
Xét \(\Delta BCN:\)
\(\widehat{BNC}=180^o-\left(\widehat{NBC}+\widehat{BCN}\right)=180^o-\left(\frac{\widehat{ABC}}{2}+\frac{\widehat{ABC}}{2}+\widehat{ACB}+50^o\right)\)
\(=180^o-\left(\widehat{ACB}+\widehat{ABC}+50^o\right)=180^o-\left(80^o+50^o\right)=50^o\)
Vậy ...

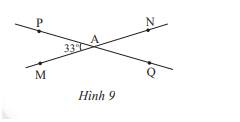
a) Ta có: \(\widehat {PAM} = \widehat {QAN}\) ( 2 góc đối đỉnh) , mà \(\widehat {PAM} = 33^\circ \)nên \(\widehat {QAN} = 33^\circ \)
Vì \(\widehat {PAN} + \widehat {PAM} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {PAN} + 33^\circ = 180^\circ \Rightarrow \widehat {PAN} = 180^\circ - 33^\circ = 147^\circ \)
Vì \(\widehat {PAN} = \widehat {QAM}\)( 2 góc đối đỉnh) , mà \(\widehat {PAN} = 147^\circ \) nên \(\widehat {QAM} = 147^\circ \)
b)
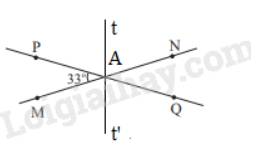
Vì At là tia phân giác của \(\widehat {PAN}\) nên \(\widehat {PAt} = \widehat {tAN} = \frac{1}{2}.\widehat {PAN} = \frac{1}{2}.147^\circ = 73,5^\circ \)
Vì \(\widehat {tAQ} + \widehat {PAt} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {tAQ} + 73,5^\circ = 180^\circ \Rightarrow \widehat {tAQ} = 180^\circ - 73,5^\circ = 106,5^\circ \)
Vẽ At’ là tia đối của tia At, ta được \(\widehat {QAt'} = \widehat {PAt}\)( 2 góc đối đỉnh)
Ta có: \(\widehat {QAt'} = \widehat {MAt'} = \frac{1}{2}.\widehat {MAQ}\) nên At’ là tia phân giác của \(\widehat {MAQ}\)
Chú ý:
2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau

a) Xét \(\Delta\)BAE và \(\Delta\)DAC có: ^BAE = ^DAC ( đối đỉnh ) ; AD = AB ( gt ) ; AE = AC ( gt )
=> \(\Delta\)BAE = \(\Delta\)DAC ( c.g.c)
=> BE = DC
b) Tương tự câu a dễ dàng cm đc: \(\Delta\)ADE = \(\Delta\)ABC => ^ADE = ^ABC => DE//BC
=> ^EDI = ^DIC mà ^EDI = ^BDI ( DI là phân giác ^BDE )
=> ^DIC = ^BDI hay ^DIB = ^IDB => \(\Delta\)BDI cân tại B.
c) Ta có: ^DBC là góc ngoài tại đỉnh B của \(\Delta\)BDI => ^DBC = ^BDI + ^BID = 2. ^BID = 2. ^CIF( theo b) (1)
Có: CF là phân giác ^BCA =>^BCF = ^ACF => ^BCA = ^BCF + ^ACF = 2. ^BCF = 2. ^ICF (2)
Lại có: ^CFD là góc ngoài của \(\Delta\)FCI => ^CFD = ^CIF + ^ICF (3)
Từ (1) ; (2) ; (3) => 2 .^CFD = 2 ^CIF + 2. ^ICF = ^DBC + ^BCA = ^DBC + ^CED ( ^CED = ^BCA vì ED //BC )