Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. + Vì \(PAM\) và \(MAQ\) là hai góc kề bù , ta có :
\(MAQ=180^0_{ }-33^0_{ }\)
\(MAQ=147^0_{ }\)
+Vì \(PAM\) đối đỉnh với \(NAQ\) nên \(NAQ=33^0_{ }\)
+ \(PAN\) đối đỉnh với \(MAQ\) nên \(PAN=147^0_{ }\)
b. +Vì \(AT\) là tia phân giác của \(PAN\) nên :
\(PAT=TAN=\dfrac{1}{2}PAN=\dfrac{147}{2}=73,5^0_{ }\)
Vì \(TAN\) và \(TAQ\) là hai góc kề bù, ta có :
\(TAN+NAQ=73,5^0_{ }+33^0_{ }\)
\(TAQ=106,5^0_{ }\)
Vì \(MAQ\) đối đỉnh với \(PAN\) nên \(MAQ=PAN\left(=147^0_{ }\right)\)
+ Vì \(AT\) là tia phân giác của \(PAN\) nên :
(1)\(PAT=TAN\)
Vì \(AT'\) là tia đối của tia \(AT\) nên :
(2)\(PTA=T'AQ\)
(3)\(TAN=MAT'\)
\(\Leftrightarrow\) Hai góc đối đỉnh
(4)Từ (1),(2),(3) suy ra \(MAT'=T'AQ\)
Do (4) và vì tia \(AT'\) nằm giữa hai tia \(AM-AQ\) (công nhận qua hình vẽ) nên \(AT'\) là tia phân giác của \(MAQ\).

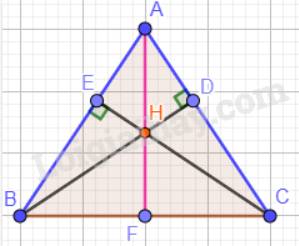
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).
Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ - 70^\circ - 70^\circ = 40^\circ \).
b) Xét tam giác vuông ADB và tam giác vuông AEC có:
AB = AC (tam giác ABC cân);
\(\widehat A\) chung.
Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).
c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.
Xét hai tam giác vuông AFB và AFC có:
AB = AC (tam giác ABC cân);
AF chung.
Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).
Vậy tia AH là tia phân giác của góc BAC.
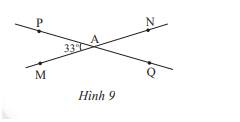

a) Ta có: \(\widehat {PAM} = \widehat {QAN}\) ( 2 góc đối đỉnh) , mà \(\widehat {PAM} = 33^\circ \)nên \(\widehat {QAN} = 33^\circ \)
Vì \(\widehat {PAN} + \widehat {PAM} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {PAN} + 33^\circ = 180^\circ \Rightarrow \widehat {PAN} = 180^\circ - 33^\circ = 147^\circ \)
Vì \(\widehat {PAN} = \widehat {QAM}\)( 2 góc đối đỉnh) , mà \(\widehat {PAN} = 147^\circ \) nên \(\widehat {QAM} = 147^\circ \)
b)
Vì At là tia phân giác của \(\widehat {PAN}\) nên \(\widehat {PAt} = \widehat {tAN} = \frac{1}{2}.\widehat {PAN} = \frac{1}{2}.147^\circ = 73,5^\circ \)
Vì \(\widehat {tAQ} + \widehat {PAt} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {tAQ} + 73,5^\circ = 180^\circ \Rightarrow \widehat {tAQ} = 180^\circ - 73,5^\circ = 106,5^\circ \)
Vẽ At’ là tia đối của tia At, ta được \(\widehat {QAt'} = \widehat {PAt}\)( 2 góc đối đỉnh)
Ta có: \(\widehat {QAt'} = \widehat {MAt'} = \frac{1}{2}.\widehat {MAQ}\) nên At’ là tia phân giác của \(\widehat {MAQ}\)
Chú ý:
2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau