Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{A'B'}{3}=\dfrac{B'C'}{14}=\dfrac{C'A'}{13}=\dfrac{A'B'+B'C'+C'A'}{3+14+13}=\dfrac{90}{30}=3\)
Do đó: A'B'=9cm; B'C'=42cm; C'A'=39cm

a) Vì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số đồng dạng \(k\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = k;\,\,\widehat B = \widehat {B'}\)
Mà AM và A’M’ lần lượt là trung tuyến của hai tam giác ABC và A’B’C’ nên M và M’ lần lượt là trung điểm của BC và B’C’.
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}BC;\,\,B'M' = \frac{1}{2}B'C'\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BM}}{{B'M'}} = k\end{array}\)
Xét tam giác ABM và tam giác A’B’M’ có:
\(\frac{{AB}}{{A'B'}} = \frac{{BM}}{{B'M'}}\) và \(\widehat B = \widehat {B'}\)
\( \Rightarrow \Delta ABM \backsim \Delta A'B'M'\) (c-g-c)
\( \Rightarrow \frac{{AM}}{{A'M'}} = \frac{{BM}}{{B'M'}} = k\)
b) Vì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số đồng dạng \(k\) nên \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = k;\,\,\widehat B = \widehat {B'}\)
\(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Vì AD và A’D’ lần lượt là phân giác của tam giác ABC và tam giác A’B’C’ nên ta có \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) và \(\frac{{D'B'}}{{D'C'}} = \frac{{A'B'}}{{A'C'}}\)
\( \Rightarrow \frac{{DB}}{{DC}} = \frac{{D'B'}}{{D'C'}} \Rightarrow \frac{{DB}}{{D'B'}} = \frac{{DC}}{{D'C'}} = \frac{{DB + DC}}{{D'B' + D'C'}} = \frac{{BC}}{{B'C'}}\)
Mà \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (chứng minh ở câu a) nên \(\frac{{DB}}{{D'B'}} = \frac{{AB}}{{A'B'}}\)
Xét tam giác ABD và tam giác A’B’D’ có:
\(\frac{{BD}}{{B'D'}} = \frac{{AB}}{{A'B'}}\) và \(\widehat B = \widehat {B'}\)
\( \Rightarrow \Delta ABD \backsim \Delta A'B'D'\) (c-g-c)
\( \Rightarrow \frac{{AD}}{{A'D'}} = \frac{{AB}}{{A'B'}} = k\)
c) Ta có \(\widehat B = \widehat {B'}\) và \(\widehat {AHB} = \widehat {A'H'B'} = 90^\circ \)
\( \Rightarrow \Delta ABH \backsim \Delta A'B'H'\) (g-g)
\( \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AH}}{{A'H'}} = k\)

Câu 3:
Xét ΔAMN và ΔABC có
AM/AB=AN/AC
\(\widehat{A}\) chung
DO đó: ΔAMN\(\sim\)ΔABC

Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {A'} = \widehat A = 90^\circ \)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (c-g-c)

Vì \(MN\parallel B'C'\) nên \(\widehat {A'MN} = \widehat {A'B'C'}\) (hai góc đồng vị)
\( \Rightarrow \widehat M = \widehat B\)
Xét tam giác A’MN và tam giác ABC có:
\(\widehat {A'} = \widehat A;\,\,A'M = AB;\,\,\widehat M = \widehat B\)
\( \Rightarrow \Delta A'MN = \Delta ABC\) (g-c-g)
Vì \(MN\parallel B'C'\) nên \(\Delta A'MN \backsim \Delta A'BC\)
\( \Rightarrow \Delta ABC \backsim \Delta A'BC\)
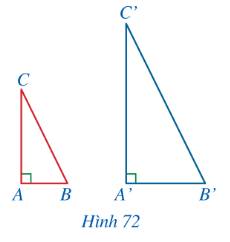

Vì \(\Delta A'B'C' \backsim \Delta ABC\) nên ta có:
\(\left\{ \begin{array}{l}A'B' = AB = 3\\B'C' = BC = 2\end{array} \right.\)
Vậy \(x = 3\) và \(y = 2\).