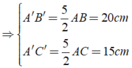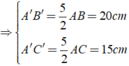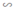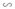Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phạm tuấn Đạt
cái này áp dụng t/c tam giác đồng dạng :Tỉ số diện tích của 2 tam giác đồng dạng bằng bình phương tỉ số đồng dạng

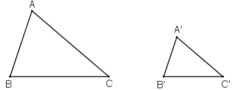
a) Gọi chu vi tam giác A’B’C’ là P’ và chu vi tam giác ABC là P.
ΔA'B'C' 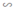 ΔABC theo tỉ số đồng dạng k = 3/5
ΔABC theo tỉ số đồng dạng k = 3/5
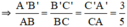
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
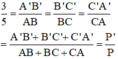
Vậy tỉ số chu vi tam giác A’B’C’ và tam giác ABC là 3/5
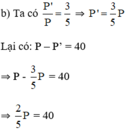
⇒ P = 100 ⇒ P’ = 60.
Vậy chu vi tam giác ABC bằng 100dm và chu vi tam giác A’B’C’ là 60dm.

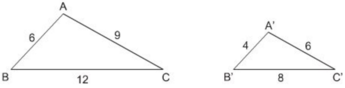
a) Ta có:
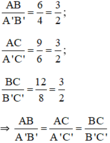
⇒ ΔABC  ΔA’B’C’ (c.c.c).
ΔA’B’C’ (c.c.c).
b) Ta có:
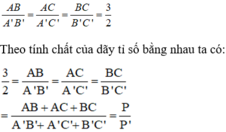
Vậy tỉ số chu vi của tam giác ABC và chu vi của tam giác A’B’C’ là 3/2.

ΔA'B'C'  ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒
ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒ 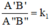
ΔA''B''C'' 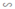 ΔABC theo tỉ số đồng dạng k2 ⇒
ΔABC theo tỉ số đồng dạng k2 ⇒ 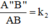
Mà ΔA'B'C' 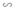 ΔA''B''C''; ΔA''B''C''
ΔA''B''C''; ΔA''B''C'' 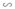 ΔABC
ΔABC
⇒ ΔA'B'C' 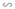 ΔABC (theo tính chất 3)
ΔABC (theo tính chất 3)
Tỉ số đồng dạng:
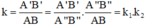
Vậy tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k1.k2.
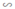 ΔABC theo tỉ số đồng dạng k = 3/5.
ΔABC theo tỉ số đồng dạng k = 3/5.