Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Xét ΔABC có
\(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{25}{13}\left(cm\right)\\CH=\dfrac{144}{13}\left(cm\right)\end{matrix}\right.\)
Bài 1:
Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{25}{36}=900\)
\(\Leftrightarrow HC=36\left(cm\right)\)
hay HB=25(cm)

\(1,\dfrac{AB}{AC}=\dfrac{5}{6}\Leftrightarrow AB=\dfrac{5}{6}AC\)
Áp dụng HTL tam giác
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{900}=\dfrac{1}{\dfrac{25}{36}AC^2}+\dfrac{1}{AC^2}\\ \Leftrightarrow\dfrac{1}{900}=\dfrac{36}{25AC^2}+\dfrac{1}{AC^2}\\ \Leftrightarrow\dfrac{1}{900}=\dfrac{36+25}{25AC^2}\Leftrightarrow\dfrac{1}{900}=\dfrac{61}{25AC^2}\\ \Leftrightarrow25AC^2=54900\Leftrightarrow AC^2=2196\Leftrightarrow AC=6\sqrt{61}\left(cm\right)\\ \Leftrightarrow AB=\dfrac{5}{6}\cdot6\sqrt{61}=5\sqrt{61}\\ \Leftrightarrow BC=\sqrt{AB^2+AC^2}=61\left(cm\right)\)
Áp dụng HTL tam giác:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=...\\CH=\dfrac{AC^2}{BC}=...\end{matrix}\right.\)
Bài 1:
Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{25}{36}=900\)
\(\Leftrightarrow HC=36\left(cm\right)\)
hay HB=25(cm)

a: Xét ΔABC vuông tại A có
AB^2+AC^2=BC^2
=>AC^2=BC^2-AB^2=144
=>AC=12cm
Xét ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC
=>AH*13=5*12=60
=>AH=60/13(cm)
Xét ΔABC vuông tại A có
sin ABC=AC/BC=12/13
nên \(\widehat{ABC}\simeq67^023'\)

Ta có:
\(sinC=\dfrac{AB}{BC}\Rightarrow sin30^o=\dfrac{AB}{5}\)
\(\Rightarrow AB=5\cdot sin30^o=\dfrac{5}{2}\left(cm\right)\)
Mà: \(tanC=\dfrac{AB}{AC}\Rightarrow tan30^o=\dfrac{\dfrac{5}{2}}{AC}\)
\(\Rightarrow AC=\dfrac{\dfrac{5}{2}}{tan30^o}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
Theo hệ thức đường cao cạnh góc vuông và cạnh huyền ta có:
\(AB\cdot AC=AH\cdot BC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{\dfrac{5}{2}\cdot\dfrac{5\sqrt{3}}{2}}{5}=\dfrac{5\sqrt{3}}{4}\left(cm\right)\)
Ta có: \(\left\{{}\begin{matrix}HB=\dfrac{AB^2}{BC}=\dfrac{\left(\dfrac{5}{2}\right)^2}{5}=\dfrac{5}{4}\left(cm\right)\\HC=\dfrac{AC^2}{BC}=\dfrac{\left(\dfrac{5\sqrt{3}}{2}\right)^2}{5}=\dfrac{15}{4}\left(cm\right)\end{matrix}\right.\)
 a) ∠ABC = 90⁰ - 30⁰ = 60⁰
a) ∠ABC = 90⁰ - 30⁰ = 60⁰
sinC = AB/BC
⇒ AB = BC.sinC
= 5.sin30⁰
= 5.1/2
= 5/2 (cm)
sinB = AC/BC
⇒ AC = BC.sinB
= 5.sin60⁰
= 5√3/2 (cm)
Ta có:
AH.BC = AB.AC
⇒ AH = AB.AC : BC
= 5/2 . 5√3/2 : 5
= 5√3/4 (cm)
AB² = BH.BC
⇒ BH = AB² : BC
= (5/2)² : 5
= 5/4 (cm)
⇒ CH = BC - BH
= 5 - 5/4
= 15/4 (cm)
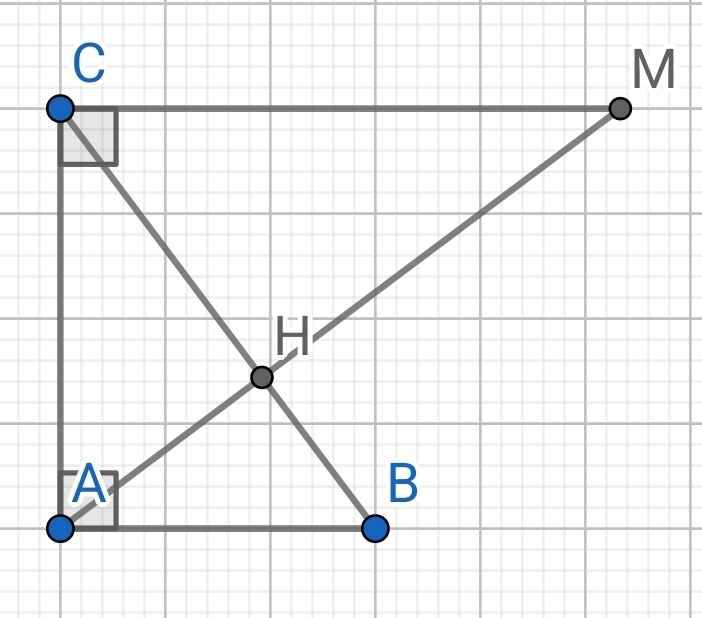
b) Do AH ⊥ BC (gt)
⇒ CH ⊥ AM
∆ACM vuông tại C có CH là đường cao
⇒ AC² = AH . AM (1)
∆ABC vuông tại A có AH là đường cao
⇒ AC² = CH . CB (2)
Từ (1) và (2) ⇒ AH.AM = CH.CB

Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)


Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
hay AC=8(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=4,8\left(cm\right)\\BH=3,6\left(cm\right)\\CH=6,4\left(cm\right)\end{matrix}\right.\)

1) Mình làm rồi nhé:
https://hoc24.vn/cau-hoi/cho-dabc-can-tai-a-co-bc-5cm-b-c-40-tinh-ab-va-duong-cao-ah.8311486416239
2) Xét tam giác vuông ABH ta có:
\(cosB=\dfrac{AH}{AB}\)
\(\Rightarrow cos60^o=\dfrac{5}{AB}\Rightarrow AB=\dfrac{5}{cos60^o}=10\)
Áp dụng định lý Py-ta-go vào tam giác này ta có:
\(AB^2=AH^2+BH^2\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{10^2-5^2}=5\sqrt{3}\)
Mà: \(BH+CH=BC\)
\(\Rightarrow CH=BC-BH=10-5\sqrt{3}\approx1,3\)
Áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{CH^2+AH^2}=\sqrt{1,3^2+5^2}\approx5,2\)

Ta có: \(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\)
Ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=\dfrac{12}{5}\left(cm\right)\)
Ta có: \(AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{4^2}{5}=\dfrac{16}{5}\left(cm\right)\)
Lời giải:
Áp dụng định lý Pitago:
$AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$CH=BC-BH=5-1,8=3,2$ (cm)

Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=12(cm)
Xét ΔACB vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}CH=\dfrac{144}{13}\left(cm\right)\\AH=\dfrac{60}{13}\left(cm\right)\end{matrix}\right.\)
C.ơn bn nhìu nha