
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


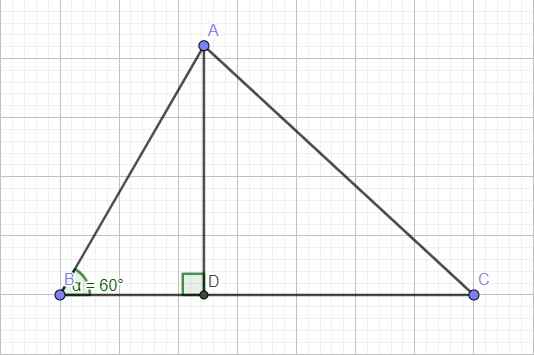
Kẻ đường cao AD, đặt \(AB=x>0\) ; \(BD=y>0\)
\(\Rightarrow AC=12-x\) ; \(CD=8-y\)
Trong tam giác vuông ABD:
\(BD=AB.cosB\Leftrightarrow y=x.cos60^0=\dfrac{x}{2}\) \(\Rightarrow CD=8-\dfrac{x}{2}\)
Theo định lý Pitago:
\(\left\{{}\begin{matrix}AD^2=AB^2-BD^2\\AD^2=AC^2-CD^2\end{matrix}\right.\) \(\Rightarrow AB^2-BD^2=AC^2-CD^2\)
\(\Leftrightarrow x^2-\left(\dfrac{x}{2}\right)^2=\left(12-x\right)^2-\left(8-\dfrac{x}{2}\right)^2\)
\(\Leftrightarrow16x-80=0\)
\(\Rightarrow x=5\)
Vậy \(\left\{{}\begin{matrix}AB=5\\AC=7\end{matrix}\right.\)

\(cosA=\dfrac{AB^2+AC^2-BC^2}{2.AB.AC}=\dfrac{5^2+8^2-7^2}{2.5.8}=\dfrac{1}{2}\\ \Rightarrow\widehat{A}=60^o\\ cosB=\dfrac{AB^2+BC^2-AC^2}{2.AB.BC}=\dfrac{5^2+7^2-8^2}{2.5.7}=\dfrac{1}{7}\\ \Rightarrow\widehat{B}=81^o47'\\ cosC=\dfrac{AC^2+BC^2-AB^2}{2.AC.BC}=\dfrac{8^2+7^2-5^2}{2.8.7}=\dfrac{11}{14}\\ \Rightarrow\widehat{C}=38^o13'\)
\(cosA=\dfrac{5^2+8^2-7^2}{2\cdot5\cdot8}=\dfrac{1}{2}\)
=>góc A=60 độ
AB/sinC=AC/sinB=BC/sinA
=>5/sinC=8/sinB=7/sin60
=>góc C=38 độ; góc B=82 độ


Dựng \(AH\) vuông góc \(BC\). Đặt \(AB=x\Rightarrow AH=x.\sin60^0=\dfrac{x\sqrt{3}}{2};BH=x\cos60^0=\dfrac{x}{2}\)
\(\Rightarrow HC=BC-BH=8-\dfrac{x}{2};AC=12-x\)
Tam giác \(AHC\) vuông tại \(H\Rightarrow AC^2=AH^2+HC^2\Rightarrow\left(12-x\right)^2=\dfrac{3x^2}{4}+\left(8-\dfrac{x}{2}\right)^2\)
Giải phương trình trên ta được \(x=5\).
Vậy \(AB=5cm\).

p dụng định lí hàm số cos của tam giác thường ta có:
AC² = AB² + BC² - 2AB.AC.c0s60*
13² = AB² + BC² - AB.BC (1)
giả thiết: BC - AB = 7 --> BC = 7 + AB thay vào (1)
1<=> 169 = AB² + (7 + AB²) - AB(7 + AB)
<=> 169 = AB² + 49 + 14AB + AB² - 7AB - AB²
<=> AB² + 7AB - 120 = 0
<=> AB = 8 --> BC = 15
.......AB = -15 ( LOẠI, cạnh không âm)

Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)

a: Xét ΔBAE có BA=BE
nên ΔBAE cân tại B
mà \(\widehat{B}=60^0\)
nên ΔABE đều
\(\Leftrightarrow AH=\dfrac{a\sqrt{3}}{2}\)

bài này của lớp 9 hả bn?