Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Áp dụng công thức tính chu kì dao động của con lắc đơn
Cách giải:
Ta có T = 2 π l g => Chu kì không phụ thuộc vào khối lượng vật => khi tăng khối lượng vật lên 4 lần thì chu kì dao động không thay đổi => Chọn D

Ta có T=\(2\pi\sqrt{\dfrac{m}{k}}\)
=>T tỉ lệ thuận với \(\sqrt{m}\)
=>T giảm đi 1 nửa khi \(\sqrt{m}\) giảm đi 2 lần => m giảm 4 lần
chọn A


T=0.4s => denta l=4 cm
thời gian dãn gấp 2 lần thời gian nén nên tnen = T/3
nếu chọn chiều (+) hướng xuống thì vị trí mà lo xo dãn là từ 2pi/3 -> 4pi/3
nên A = 8 cm

Đáp án D
Chu kì con lắc sau khi thay đổi: T ' = 2 π 2 l ' g = 2 . 2 π l g = 2 T
(Chu kì không phụ thuộc vào khối lượng vật nặng)

Đáp án A
Phương pháp: Sử dụng công thức tính chu kì của con lắc đơn
Cách giải:
Chu kì của con lắc đơn T = 2 π l g
Nếu chiều dài l của con lắc tăng lên 4 lần thì chu kì của con lắc tăng lên 4 = 2 lần

Đáp án C
Phương pháp: Áp dụng công thức tính chu kỳ của con lắc đơn 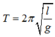
Áp dụng công thức tính chu kỳ của con lắc đơn ta thâý khi chiều dài của con lắc tăng 4 lần thì chu kỳ tăng lên 2 lần
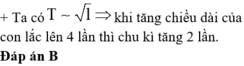
Ta có T ~ 1 ⇒ tăng chiều dài lên 4 lần thì chu kì con lắc tăng 2 lần. Chú ý rằng chu kì dao động của con lắc đơn không phụ thuộc vào khối lượng.
Đáp án A