Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có T=\(2\pi\sqrt{\dfrac{m}{k}}\)
=>T tỉ lệ thuận với \(\sqrt{m}\)
=>T giảm đi 1 nửa khi \(\sqrt{m}\) giảm đi 2 lần => m giảm 4 lần
chọn A

Chu kì riêng của con lắc: \(T=2\pi\sqrt{\frac{l}{g}}=2,8s\)
Vậy khi chu kì của ngoại lực tăng từ 2s đến 4s thì biên độ ̣con lắc tăng rồi giảm
Đáp án D

Đáp án B
Phương pháp: Áp dụng công thức tính chu kì dao động của con lắc đơn T = 2 π l g
Cách giải:
Khi gia tốc trọng trường giảm 4,5 lần, chiều dài dây treo giảm 2 lần thì:
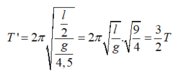
Vậy chu kì tăng lên 1,5 lần

Gia tốc biểu kiến của con lắc nằm trong thang máy chuyển động với gia tốc \(\overrightarrow a\) là:
\(\overrightarrow {g'} = \overrightarrow {g} -\overrightarrow a \)
Thang máy đi lên chậm dần đều nên \(\overrightarrow g \uparrow \uparrow \overrightarrow a\) => \( {g'} ={g} -a \)
Mà \(a = \frac{g}{2} => g' = g - \frac{g}{2} = \frac{g}{2}.\)
Chu kì của con lắc lúc này là \(T' =2\pi \sqrt{\frac{l}{g}} = 2\pi \sqrt{\frac{2l}{g}} = T\sqrt{2}.\)

\(T=2\pi\sqrt{\frac{l}{g}}\)
\(T'=2\pi\sqrt{\frac{l'}{g}}\)
\(\Rightarrow\frac{T'}{T}=\sqrt{\frac{l'}{l}}=\sqrt{2}\Rightarrow T'=2\sqrt{2}s\)

Ta có T ~ 1 ⇒ tăng chiều dài lên 4 lần thì chu kì con lắc tăng 2 lần. Chú ý rằng chu kì dao động của con lắc đơn không phụ thuộc vào khối lượng.
Đáp án A
Đáp án D
Chu kì con lắc sau khi thay đổi: T ' = 2 π 2 l ' g = 2 . 2 π l g = 2 T
(Chu kì không phụ thuộc vào khối lượng vật nặng)