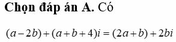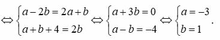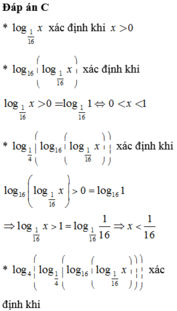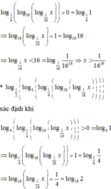Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Gọi $d$ là ƯCLN của $a$ và $b$. Khi đó $a=dx, b=dy$ với $x,y$ nguyên dương và nguyên tố cùng nhau
Ta có:
$d=15$
BCNN$(a,b)=dxy=2835$
$\Rightarrow xy=189$
Mà $x,y$ là 2 số nguyên dương nguyên tố cùng nhau nên $(x,y)=(1,189), (189,1), (27,7), (7,27)$
$\Rightarrow (a,b)=(15,2835), (2835, 15), (405,105), (105,405)$

Ta có : \(\left(a^{\log_37}\right)^{\log_37}+\left(b^{\log_711}\right)^{\log_711}+\left(c^{\log_{11}25}\right)^{\log_{11}25}=27^{^{\log_37}}+49^{^{\log_711}}+\left(\sqrt{11}\right)^{^{\log_{11}25}}\)
\(=7^3+11^2+25^{\frac{1}{2}}=469\)

Lời giải:
Áp dụng BĐT Cô-si:
\(2=a+b=\frac{a}{2}+\frac{a}{2}+b\geq 3\sqrt[3]{\frac{a^2b}{4}}\)
\(\Rightarrow \frac{2}{3}\geq \sqrt[3]{\frac{a^2b}{4}}\Rightarrow \frac{8}{27}\geq \frac{a^2b}{4}\)
\(\Leftrightarrow a^2b\leq \frac{32}{27}\Leftrightarrow P\leq \frac{32}{27}\)
Vậy $P_{\max}=\frac{32}{27}$. Giá trị này đạt tại $\frac{a}{2}=b=\frac{2}{3}$

\(P=\dfrac{1}{log_a\dfrac{a}{b}}+log_bb-log_ba=\dfrac{1}{1-log_ab}+1-log_ba\)
\(=\dfrac{log_ba}{log_ba-1}+1-log_ba\)
Đặt \(log_ba=x\Rightarrow x\ge2\)
\(P=f\left(x\right)=\dfrac{x}{x-1}+1-x\)
\(f'\left(x\right)=\dfrac{-1}{\left(x-1\right)^2}-1< 0\) \(\Rightarrow\) hàm nghịch biến
\(\Rightarrow P\) chỉ tồn tại max (tại \(x=2\)), ko tồn tại min
Đề sai

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0
⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0
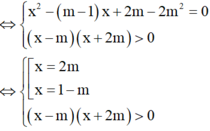
Điều kiện để pt đã cho có 2 nghiệm
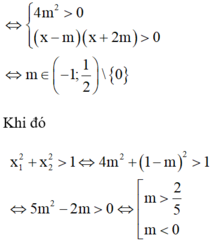
Do đó
S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2

Ta có OA = OB nên tập hợp các tâm O của các mặt cầu đi qua hai điểm A, B là mặt phẳng trung trực của đoạn AB
Đáp án:B