Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
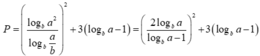
Đặt t= logba-1 > logbb -1=0 ,
khi đó:
P = 2 t + 2 t 2 + 3 t = f ( t ) f ' t = 2 . 2 t + 2 t . - 2 t 2 + 3 = 3 t 3 - 8 ( t + 1 ) t 3
F’ (t) =0 khi 3t3-8( t+1) =0 hay t= 2.
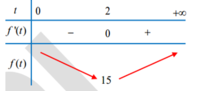
Suy ra Pmin =f(2) =15
Chọn D.

Chọn D.
Ta có:
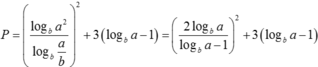
Đặt t = logba – 1 > logbb – 1 = 0; khi đó:
![]()
Ta có: ![]()
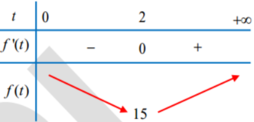
Và f’(t) = 0 khi 3t3 - 8( t + 1) = 0 hay t = 2.
Suy ra Pmin = f(2) = 15

Đặt \(log_9a=log_{12}b=log_{15}\left(a+b\right)=t\Rightarrow\left\{{}\begin{matrix}a=9^t\\b=12^t\\a+b=15^t\end{matrix}\right.\)
\(\Rightarrow9^t+12^t=15^t\)
\(\Rightarrow\left(\dfrac{3}{5}\right)^t+\left(\dfrac{4}{5}\right)^t=1\)
Hàm \(f\left(t\right)=\left(\dfrac{3}{5}\right)^t+\left(\dfrac{4}{5}\right)^t\) có \(f'\left(t\right)=\left(\dfrac{3}{5}\right)^tln\left(\dfrac{3}{5}\right)+\left(\dfrac{4}{5}\right)^t.ln\left(\dfrac{4}{5}\right)< 0\Rightarrow\) nghịch biến trên R
\(\Rightarrow f\left(t\right)\) có tối đa 1 nghiệm \(\Rightarrow t=2\) là nghiệm duy nhất
\(\Rightarrow\dfrac{a}{b}=\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16}\)
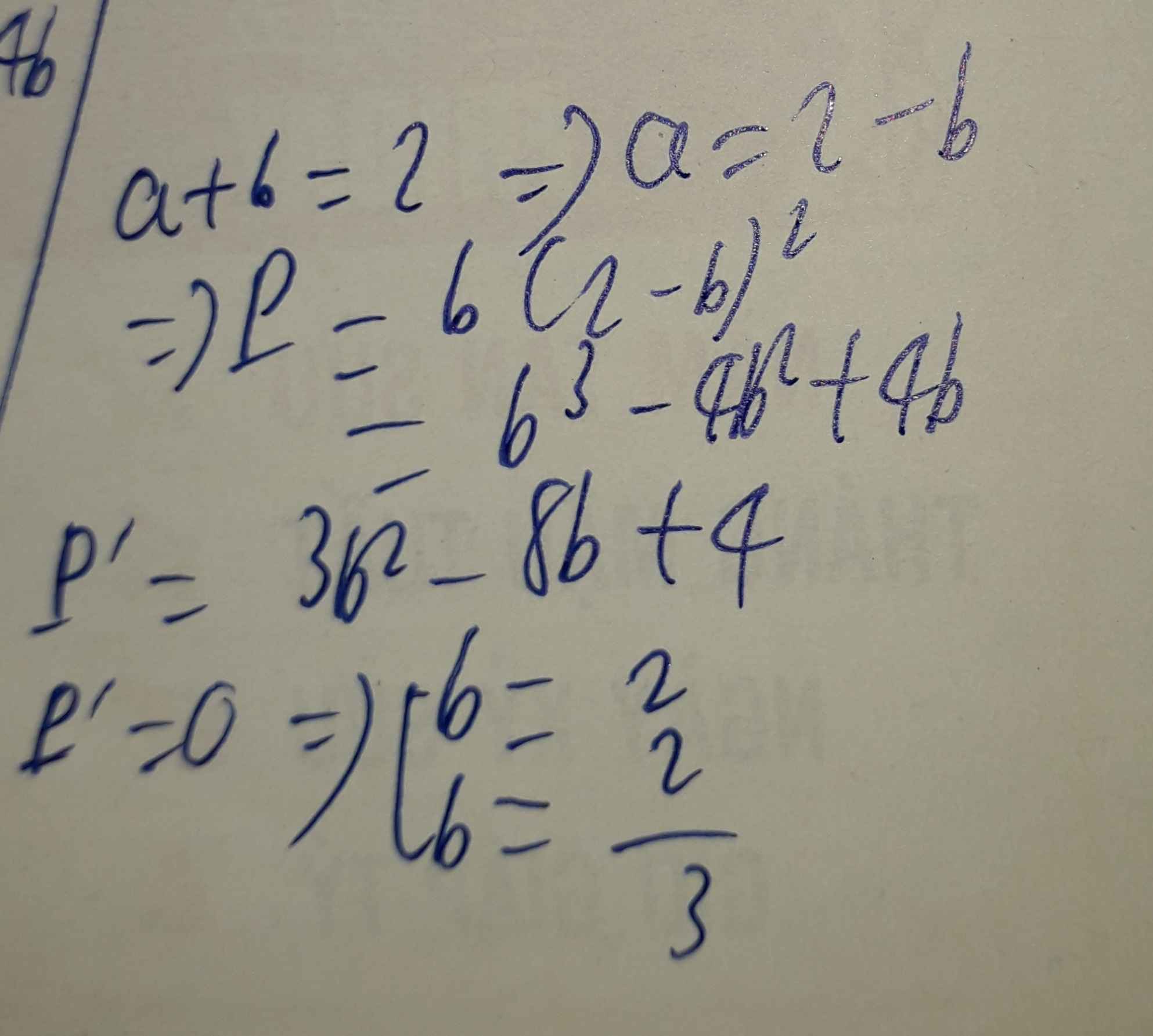
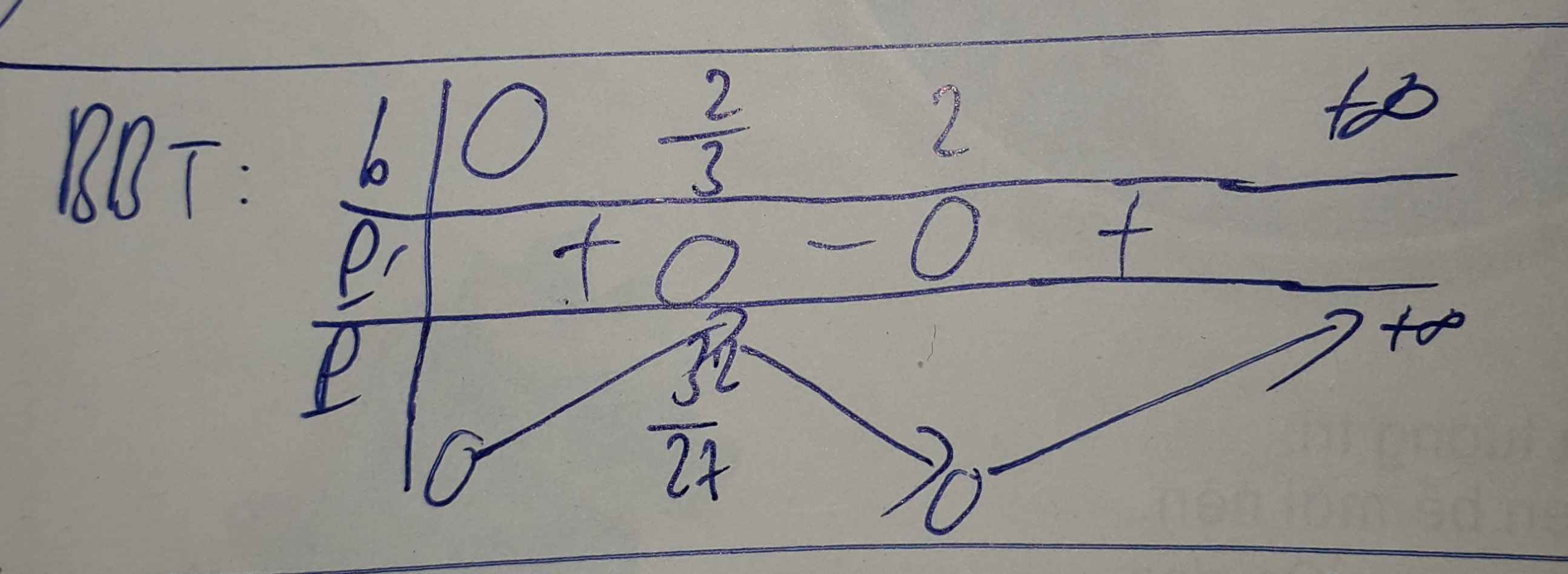
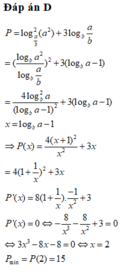
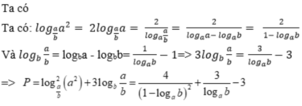
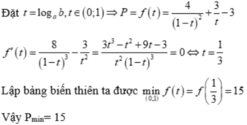
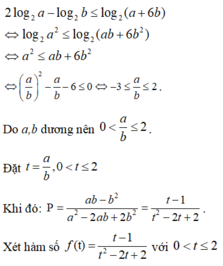
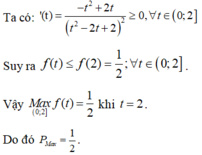
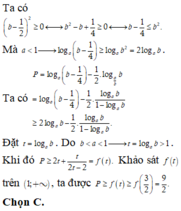
Lời giải:
Áp dụng BĐT Cô-si:
\(2=a+b=\frac{a}{2}+\frac{a}{2}+b\geq 3\sqrt[3]{\frac{a^2b}{4}}\)
\(\Rightarrow \frac{2}{3}\geq \sqrt[3]{\frac{a^2b}{4}}\Rightarrow \frac{8}{27}\geq \frac{a^2b}{4}\)
\(\Leftrightarrow a^2b\leq \frac{32}{27}\Leftrightarrow P\leq \frac{32}{27}\)
Vậy $P_{\max}=\frac{32}{27}$. Giá trị này đạt tại $\frac{a}{2}=b=\frac{2}{3}$