Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng hằng đẳng thức \(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
\(M=\left(b^2+c^2-a^2\right)^2-4b^2c^2=\left(b^2+c^2-2bc-a^2\right)\left(b^2+c^2+2bc-a^2\right)=\left[\left(b-c\right)^2-a^2\right].\left[\left(b+c\right)^2-a^2\right]=\left(b-c-a\right)\left(b-c+a\right)\left(b+c-a\right)\left(b+c+a\right)\)
b) Nếu a,b,c là độ dài các cạnh của tam giác thì ta có : \(\hept{\begin{cases}a+b>c>0\\b+c>a>0\\a+c>b>0\end{cases}\Leftrightarrow\hept{\begin{cases}b-c-a< 0\left(1\right)\\b-c+a>0\left(2\right)\\b+c-a>0\left(3\right)\end{cases}}}\)
Nhân (1) , (2) , (3) theo vế cùng với a+b+c>0 được M<0
c) Dễ thấy rằng : Trong phân tích M thành nhân tử, ta thấy có xuất hiện thừa số (a+b+c)
Mà a+b+c chia hết cho 6 nên suy ra M chia hết cho 6

a: \(A=\left(b^2+c^2-a^2\right)^2-4b^2c^2\)
\(=\left(b^2+c^2-a^2\right)^2-\left(2bc\right)^2\)
\(=\left(b^2-2bc+c^2-a^2\right)\left(b^2+2bc+c^2-a^2\right)\)
\(=\left[\left(b+c\right)^2-a^2\right]\left[\left(b-c\right)^2-a^2\right]\)
\(=\left(b+c-a\right)\left(b+c+a\right)\left(b-c-a\right)\left(b-c+a\right)\)
b: a,b,c là độ dài 3 cạnh của 1 tam giác
=>b+c>a và a+b>c và a+c>b
=>b+c-a>0 và a+b-c>0 và a+c-b>0
=>b+c-a>0 và b-(c+a)<0 và a+b-c>0
=>(b+c-a)[b-(c+a)][a+b-c](a+b+c)<0
=>A<0

Ta có
D = a ( b 2 + c 2 ) – b ( c 2 + a 2 ) + c ( a 2 + b 2 ) – 2 a b c = a b 2 + a c 2 – b c 2 – b a 2 + c a 2 + c b 2 – 2 a b c = ( a b 2 – a 2 b ) + ( a c 2 – b c 2 ) + ( a 2 c – 2 a b c + b 2 c ) = a b ( b – a ) + c 2 ( a – b ) + c ( a 2 – 2 a b + b 2 ) = - a b ( a – b ) + c 2 ( a – b ) + c ( a – b ) 2 = ( a – b ) ( - a b + c 2 + c ( a – b ) ) = ( a – b ) ( - a b + c 2 + a c – b c ) = ( a – b ) [ ( - a b + a c ) + ( c 2 – b c ) ]
= (a – b)[a(c – b) + c(c – b)]
= (a – b)(a + c)(c – b)
Với a = 99; b = -9; c = 1, ta có
D = (99 - (-9))(99 + 1) (1 - (-9)) = 108.100.10 = 108000
Đáp án cần chọn là: B
mới ăn miếng cơm cà ngon nhức nách luôn ai thèm cơm cà không điểm danh nào

1: (a-1)(a-3)(a-4)(a-6)+9
=(a^2-7a+6)(a^2-7a+12)+9
=(a^2-7a)^2+18(a^2-7a)+81
=(a^2-7a+9)^2>=0
b: \(A=\dfrac{a^4-4a^3+a^2+4a^3-16a+4+16a-3}{a^2}=\dfrac{16a-3}{a^2}\)
a^2-4a+1=0
=>a=2+căn 3 hoặc a=2-căn 3
=>A=11-4căn 3 hoặc a=11+4căn 3
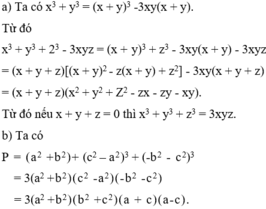

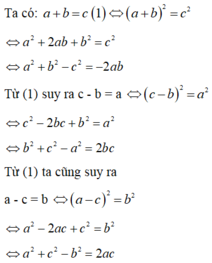

câu a làm theo hằng đẳng thức
câu b ta sẽ đc (b^2 +c^2 -a^2 -2bc )(b^2 +c^2 -a^2 +2bc ) = { (b-c)^2 -a^2 } {(b+c)^2-a^2}
theo bất đẳng thức trong tam giác thì hiệu 2 cạnh luôn nhỏ hơn cạnh còn lại nên {(b-c)^2-a^2} <0
mà {(b+c)^2-a^2} >0 \(\Rightarrow\)A<0
k cho mk cái nha
a, \(A=\left(b^2+c^2-a^2\right)-4b^2c^2\)
\(\Rightarrow A=\left(b^2+c^2-a^2\right)-\left(2bc\right)^{^2}\)
\(\Rightarrow A=\left(b^2+c^2-a^2-2bc\right)\left(b^2+c^2-a^2+2bc\right)\)
\(\Rightarrow A=\left[\left(b-c\right)^2-a^2\right]\left[\left(b+c\right)^2-a^2\right]\)
\(\Rightarrow A=\left(c-b-a\right)\left(c-b+a\right)\left(c+b-a\right)\left(c+b+a\right)\)
b, Như bạn Trần Thị Nhung