Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*) \(MinA\) :
Ta thấy: a,b,c đều là các số thực không âm.
Do đó : \(A\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=0,c=1\) và các hoán vị.
\(*)MaxA\) :
Giả sử \(a\ge b\ge c\) \(\Rightarrow3a\ge a+b+c=1\)
\(\Rightarrow1-3a\le0\)
Ta có : \(A=a\left(b^2+c^2\right)+b\left(c^2+a^2\right)+c\left(a^2+b^2\right)\)
\(=a\left(b^2+c^2\right)+b\left(c^2+a^2\right)+c\left(a^2+b^2\right)+3abc-3abc\)
\(=\left(a+b+c\right)\left(ab+bc+ca\right)-3abc\)
\(=ab+bc+ca-3abc\)
\(=a\left(b+c\right)+bc\left(1-3a\right)\) \(\le\frac{\left(a+b+c\right)^2}{4}+0\) ( do \(1-3a\le0\) ) \(=\frac{1}{4}\)
hay \(A\le\frac{1}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=\frac{1}{2},c=0\) và các hoán vị.
\(\)

Điều kiện x ≠ 0 và x ≠ -3
Ta có:
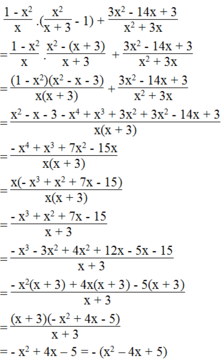
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3

Ta có thể giải bài toán này bằng cách sử dụng phương pháp điều chỉnh biểu thức P để biểu thức này có thể được phân tích thành tổng của các biểu thức có dạng a(x-y)+b(y-z)+c(z-x), trong đó x,y,z là các số thực không âm. Khi đó, ta có:
P = ab + bc - ca = a(b-c) + b(c-a) + c(a-b) = a(-c+b) + b(c-a) + c(-b+a) = a(x-y) + b(y-z) + c(z-x), với x = -c+b, y = c-a và z = -b+a
Do đó, để tìm giá trị lớn nhất của P, ta cần tìm các giá trị lớn nhất của x, y, z. Ta có:
x = -c+b ≤ b, vì c ≥ 0 y = c-a ≤ c ≤ 2022, vì a+b+c = 2022 z = -b+a ≤ a, vì b ≥ 0
Vậy giá trị lớn nhất của P là:
P_max = ab + bc - ca ≤ b(2022-a) + 2022a = 2022b
Tương tự, để tìm giá trị nhỏ nhất của P, ta cần tìm các giá trị nhỏ nhất của x, y, z. Ta có:
x = -c+b ≥ -2022, vì b ≤ 2022 y = c-a ≥ 0, vì c ≤ 2022 và a ≥ 0 z = -b+a ≥ -2022, vì a ≤ 2022
Vậy giá trị nhỏ nhất của P là:
P_min = ab + bc - ca ≥ (-2022)a + 0b + (-2022)c = -2022(a+c)
Do đó, giá trị lớn nhất của P là 2022b và giá trị nhỏ nhất của P là -2022(a+c).

a) M có nghĩa khi a 3 - 4 a ≠ 0 ⇔ a ≠ { 0 ; ± 2 }
b) Rút gọn thu được: M = a ( a 2 + 4 a + 4 ) a ( a 2 − 4 ) = a + 2 a − 2
c) M = − 3 ⇔ a + 2 a − 2 = − 3 ⇔ a = 1 (TMĐK)
cm gì vạy bạn ?
\(A=4a\left(a+b\right)\left(a+b+c\right)\left(a+c\right)+b^2c^2\)
\(=4\left[a\left(a+b+c\right)\right]\left[\left(a+b\right)\left(a+c\right)\right]+b^2c^2\)
\(=4\left[a^2+ab+ac\right]\left[a^2+ac+ab+bc\right]+b^2c^2\)
Đặt \(a^2+ab+ac=t\)
Khi đó:
\(A=4t\left[t+bc\right]+b^2c^2\)
\(=4t^2+4tbc+b^2c^2\)
\(=\left(2t+bc\right)^2=\left(2a^2+2ab+2ac+bc\right)^2\ge0\forall a;b;c\)