Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có vật AB và ảnh A1B1 cùng thật và ngược chiều, nên k1 < 0; AB → A1B1
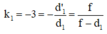
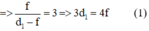
Tương ứng với vị trí sau của vật AB thật và ảnh A2B2 ảo cùng chiều nên k2 > 0.
Vật di chuyển lại gần nên d2 = d1 - 12
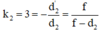
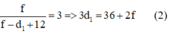
Từ (1) và (2) ta có: 4f = 36 + 2f → f = 18cm
Đáp án: B
a) Vật cho ảnh cao hơn vật thì thấu kính là thấu kính hội tụ.
b) \(d'=\dfrac{df}{d-f}\)
Độ phóng đại của ảnh: \(k=-\dfrac{d'}{d}=-\dfrac{f}{d-f}\)
Theo giả thiết:
\(\dfrac{f}{d-f}=3\)
\(\dfrac{f}{d-12-f}=-3\)
Ta suy ra hệ
\(\begin{cases}4f-3d=0\\2f-3d=-36\end{cases}\)
\(\Rightarrow f = 18cm\)
Chọn đáp án B
+ Thấu kính phân ki vật thật luôn cho ảnh ảo nhỏ hcm vật. Thấu kính hội tụ vật thật đặt trong tiêu cự cho ảnh ảo lớn hơn vật, vật thật đặt đặt cách thấu kính từ f đến 2f cho ảnh thật lớn hơn vật, và vật thật đặt cách thấu kính lớn hơn 2f cho ảnh thật nhỏ hơn vật.
+ Hai ảnh có cùng độ lớn thì một ảnh là ảnh thật (ảnh đầu) và một ảnh là ảnh ảo (ảnh sau).
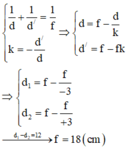
Chọn đáp án C
+ Thấu kính phân kì, vật thật luôn cho ảnh ảo cùng chiều và nhỏ hơn vật (k = + 0,5)
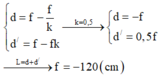
Đáp án D
Áp dụng công thức của thấu kính
1 d + 1 d ' = 1 f ↔ 1 20 + 1 − 40 = 1 f → f = 40 c m
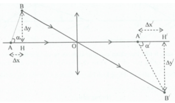
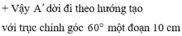
Chọn B
+ Ở vị trí thứ nhất (ảnh thật, ngược chiều) ta có:
k = -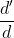
= -3 => d' = 3d.
Áp dụng công thức vị trí ta được f = 3d/4. (1)
+ Ở vị trí thứ hai (ảnh ảo, cùng chiều) ta có:
k = -
- 3 => d'' = 3d - 36.
Áp dụng công thức vị trí ta được f = 3(d -12)/2 (2)
+ Từ (1) và (2) ta suy ra d = 24; d' = 72, thế lại vào công thức vị trí ta có f = 18 cm.