Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{1+2+1}{3}=\dfrac{4}{3}\\y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{-2-1+1}{3}=-\dfrac{2}{3}\\z_G=\dfrac{z_A+z_B+z_C}{3}=\dfrac{0+1+0}{3}=\dfrac{1}{3}\end{matrix}\right.\Rightarrow G\left(\dfrac{4}{3};-\dfrac{2}{3};\dfrac{1}{3}\right)\)
\(\overrightarrow{CD}\left(-1;-3;0\right)\) la vecto phap tuyen cua mp do
\(\Rightarrow\left(P\right):-1\left(x-\dfrac{4}{3}\right)-3\left(y+\dfrac{2}{3}\right)+0=0\Leftrightarrow x+3y+\dfrac{2}{3}=0\)

Mặt phẳng ( α ) đi qua hai điểm A, B và vuông góc với mặt phẳng ( β ): x + 2y – z = 0.
Vậy hai vecto có giá song song hoặc nằm trên ( α ) là AB → = (2; 2; 1) và n β → = (1; 2; −1).
Suy ra ( α ) có vecto pháp tuyến là: n α → = (−4; 3; 2)
Vậy phương trình của ( α ) là: -4x + 3(y – 1) + 2z = 0 hay 4x – 3y – 2z + 3 = 0

Mặt phẳng ( α ) đi qua điểm D và song song với mặt phẳng (ABC) nên ( α ) cũng có vecto pháp tuyến là n ' → = (1; 1; 1)
Vậy phương trình của ( α ) là: (x – 4) + (y) + (z – 6) = 0 hay x + y + z – 10 = 0.

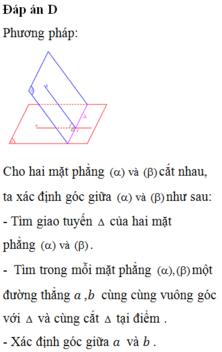
Đáp án D
Phương trình mặt phẳng trung trực của AB là ( α ) : x + z + 1 = 0
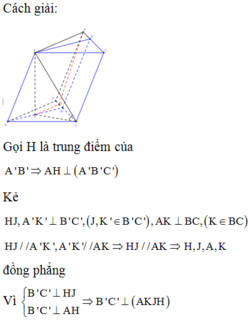
Vì tam giác ABC đều ⇒ C ∈ ( α ) mà
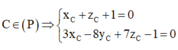
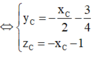
![]()
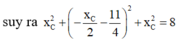
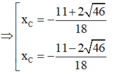
Vậy có 2 điểm C thỏa mãn yêu cầu bài toán.

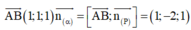


Chọn D