Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot EB=HE^2\)
b: Xét tứ giác AEHF có
\(\widehat{FAE}=\widehat{AFH}=\widehat{AEH}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: FE=AH và \(\widehat{FHE}=90^0\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot FC=FH^2\)
Áp dụng định lí Pytago vào ΔFHE vuông tại H, ta được:
\(HF^2+HE^2=FE^2\)
\(\Leftrightarrow AH^2=AE\cdot EB+AF\cdot FC\)
1) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{9+16}=\sqrt{25}=5\)(cm)
BH \(=\dfrac{AB^2}{BC}=\dfrac{9}{5}\)(cm)
\(CH=\dfrac{AC^2}{BC}=\dfrac{16}{5}\left(cm\right)\)
\(AH=\dfrac{AB.AC}{BC}=\dfrac{12}{5}\left(cm\right)\)
2) a) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được điều phải chứng minh.
b)Chứng minh tương tự câu a), ta được:
AF.FC=HF^2
Lại có:
Tứ giác AFHE có 3 góc vuông nên từ giác AFHE là hình chữ nhật.
Suy ra, HF = AE
Suy ra, AF.FC=AE^2
Mà AE.EB=HE^2
Nên AF.FC+AE.EB=AE^2+HE^2=AH^2(đpcm)
3) Áp dụng hệ thức về cạnh và góc trong tam giác, ta được:
\(BE=\cos B.BH=\cos B.\left(\cos B.AB\right)=\cos^2B.AB=\cos^2B.\left(\cos B.BC\right)=\cos^3.BC\left(đpcm\right)\)

tam giác AHB vuông tại H , đường cao HE có
AH2=AE.AB
tam giác AHC vuông tại H , đường cao HF có
AH2=AF.AC
=> AE.AB=AF.AC
Chứng minh: HB/HC = (AB/AC)2
tam giác ABC vuông tại A , đường cao AH có
AB2=HB.BC
AC2=HC.BC
\(\dfrac{AB^2}{AC^2}=\dfrac{HB.BC}{HC.BC}\)
<=> \(\dfrac{AB^2}{AC^2}=\dfrac{HB}{HC}\)
<=> HB/HC = (AB/AC)2

a: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
b: Sửa đề: \(AE\cdot EB+AF\cdot FC=HB\cdot HC\)
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
Xét ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot EB=HE^2\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot FC=HF^2\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(HB\cdot HC=AH^2\)
\(AE\cdot EB+AF\cdot FC=HE^2+HF^2\)
\(=EF^2=AH^2=HB\cdot HC\)

1: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=3^2+4^2=25\)
=>BC=5(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>AH=2,4(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\CH\cdot CA=CA^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{3^2}{5}=1,8\left(cm\right)\\CH=\dfrac{4^2}{5}=3,2\left(cm\right)\end{matrix}\right.\)
2: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF
Xét ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot EB=HE^2\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot FC=HF^2\)
\(AE\cdot EB+AF\cdot FC=HE^2+HF^2=EF^2=AH^2\)
3: Xét ΔBAC vuông tại B có \(cosB=\dfrac{BA}{BC}\)
Xét ΔBHA vuông tại H có \(cosB=\dfrac{BH}{BA}\)
Xét ΔBEH vuông tại E có \(cosB=\dfrac{BE}{BH}\)
\(cos^3B=cosB\cdot cosB\cdot cosB\)
\(=\dfrac{BA}{BC}\cdot\dfrac{BH}{BA}\cdot\dfrac{BE}{BH}=\dfrac{BE}{BC}\)
=>\(BE=BC\cdot cos^3B\)

Xét ΔFHA vuông tại F và ΔACB vuông tại A có
\(\widehat{FHA}=\widehat{ACB}\left(=90^0-\widehat{HAC}\right)\)
Do đó: ΔFHA đồng dạng với ΔACB
=>\(\dfrac{AF}{AB}=\dfrac{HA}{CB}\)
Xét tứ giác AEHF có \(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
nên AEHF là hình chữ nhật
=>AH=EF
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(EF\cdot BC=AH\cdot BC\)
Xét ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\)
\(\dfrac{AE\cdot AB}{EF\cdot BC}=\dfrac{AH^2}{AH\cdot BC}=\dfrac{AH}{BC}=\dfrac{AF}{AB}\)

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\left(1\right)\)
Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AH^2=AE\cdot AB\left(2\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AH^2=AF\cdot AC\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AE\cdot AB=AF\cdot AC=BH\cdot HC\)
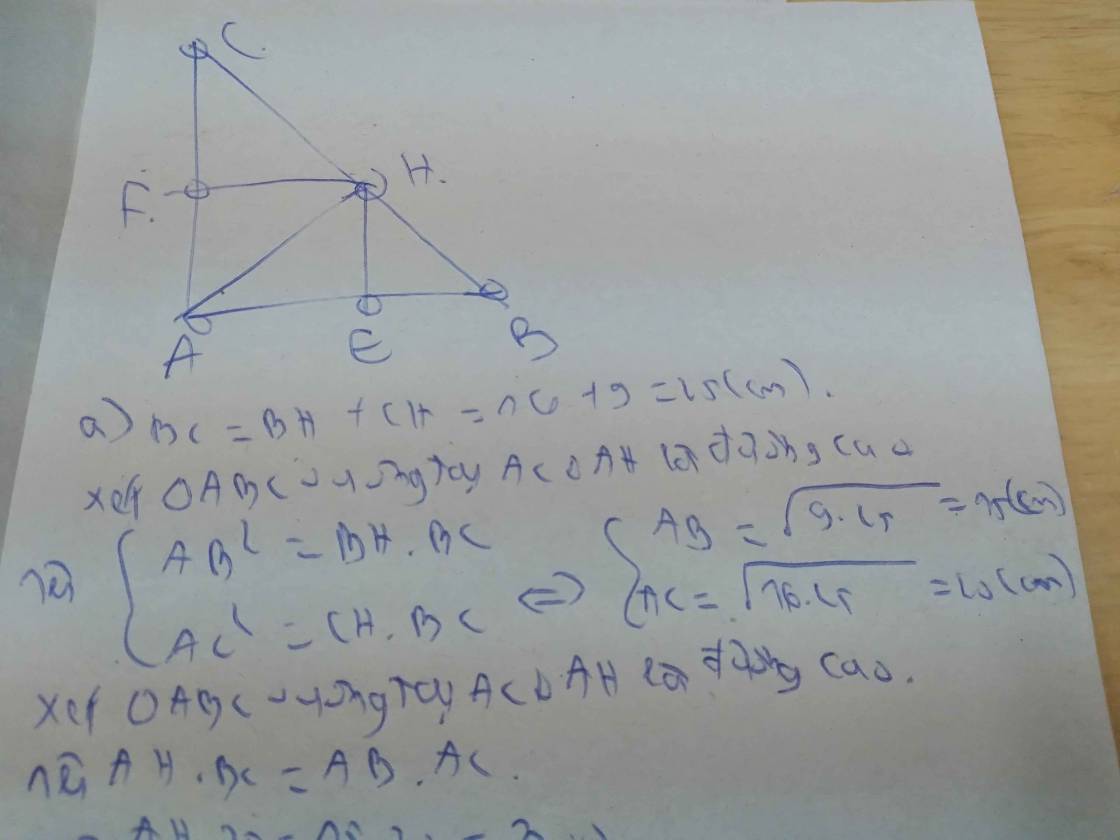

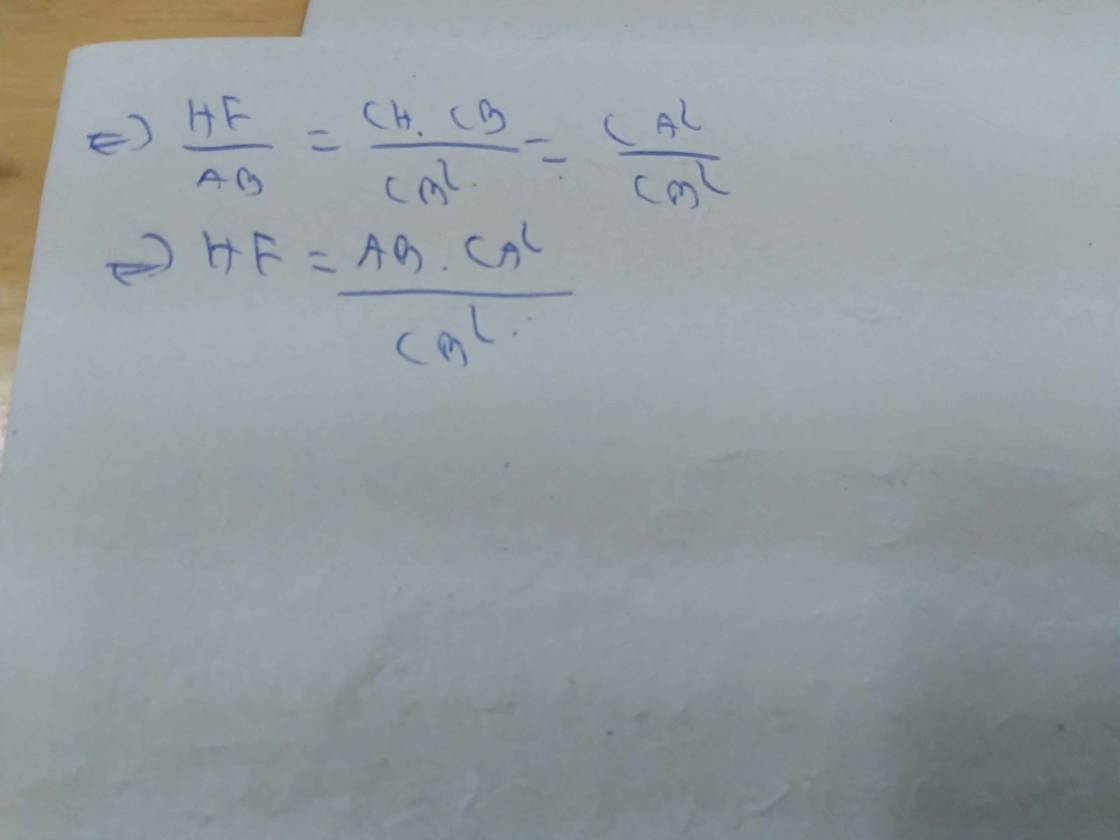
bn tự vẽ hình được chứ
bài này sẽ dựa vào hai định lí sau để giải :
1 : \(b^2=ab'\) và \(c^2=ac'\)
2.\(h^2=b'c'\)
Giải :
Áp dụng hệ thức lượng cho tam giác AHB vuông tại H có :
\(AH^2=AF.AB\) ( theo định lí 1) (1)
Áp dụng hệ thức lượng cho tam giác BAC vuông tại A có :
\(AH^2=BH.HC\) ( theo định lí 2) (2)
Từ (1) và (2) , suy ra : AF.AB = BH.HB
=> ĐPCM