Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CosB = AB / BC
SinC = AB / BC
=> CosB = SinC
Tương tự em làm các bài sau nhé !

Áp dụng hệ thức Py-ta-go vào tam giác ABC vuông tại C, ta có:
AB2=BC2+CA2=1,22+0,92=1,52 => AB = 1,5
Ta có:
- tanB = CACB = 0,91,2 = 34
- cotB = CBCA = 1,20,9 = 43
- sinB = CAAB = 0,91,5 = 35
- cosB = CBAB = 1,21,5 = 45
Vì góc A và góc B phụ nhau, nên:
- cotA = tanB = 34
- tanA = cotB = 43
- sinA = cosB = 45
- cosA = sinB = 0,91,5 = 35

Bài 2:
Gọi tam giác cần có trong đề là ΔABC vuông tại A có \(\widehat{B}=\alpha\)
Ta có: \(\tan^2B+1=\left(\dfrac{AC}{AB}\right)^2+1=\dfrac{AC^2+AB^2}{AB^2}=\dfrac{BC^2}{AB^2}\)
\(\Leftrightarrow\tan^2B+1=1:\dfrac{AB^2}{BC^2}=\dfrac{1}{\cos^2B}\)(đpcm)


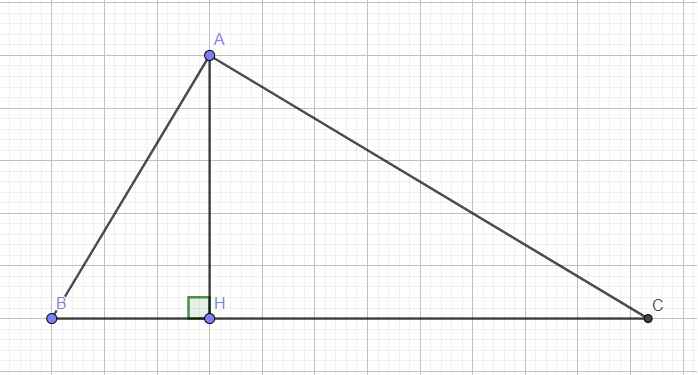
Kẻ đường cao AH
Trong tam giác vuông ABH ta có:
\(tanB=\dfrac{AH}{BH}\)
Trong tam giác vuông ACH:
\(cotC=\dfrac{CH}{AH}\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{CH}{AH}\) \(\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\)
Xét hai tam giác vuông ABH và CAH:
\(\left\{{}\begin{matrix}\dfrac{AH}{CH}=\dfrac{BH}{AH}\\\widehat{AHB}=\widehat{CHA}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta ABH\sim\Delta CAH\left(c.g.c\right)\)
\(\Rightarrow\widehat{B}=\widehat{CAH}\)
\(\Rightarrow\widehat{A}=\widehat{BAH}+\widehat{CAH}=\widehat{BAH}+\widehat{B}=90^0\)
\(\Rightarrow\Delta ABC\) vuông tại A (đpcm)