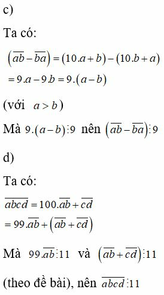NN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
3 tháng 12 2015
a. +) Nếu a, b đều chẵn: a, b có dạng: 2k ( k là số tự nhiên bất kì)
Ta có: a.b.(a+b) = 2k.2k.(2k+2k)=2k.2k.4k chia hết cho 2
+) Nếu a, b đều lẻ: a, b có dạng: 2k+1 (k là stn bất kì)
Ta có: a.b(a+b)= (2k+1).(2k+1).(2k+1+2k+1)=(2k+1).(2k+1).(4k+2)=(2k+1).(2k+1).2.(2k+1) chia hết cho 2
+) Nếu a, b một chẵn, một lẻ: a, b có dạng: 2k và 2k+1
Ta có: a.b(a+b)=2k.(2k+1).(2k+2k+1) =2k.(2k+1).(4k+1) chia hết cho 2
Vậy a.b(a+b) luôn chia hết cho 2.
b. a+b không chia hết cho 2
=> a, b là một chẵn một lẻ (vì lẻ + chẵn = lẻ không chia hết cho 2)
=> a.b là tích của 1 số chẵn và 1 số lẻ
=> a.b = 2k.(2k+1) chia hết cho 2
Vậy...
CM
17 tháng 6 2018
a, Gọi ba số tự nhiên liên tiếp là: a; a+1; a+2 tổng của ba số này bằng: a+a+1+a+2 = 3a + 3 = 3(a+1) là một số chia hết cho 3.
b, Gọi bốn số tự nhiên liên tiếp là: a; a+1; a+2; a+3 tổng của bốn số này bằng: a+a+1+a+2+a+3 = 4a+6, là một số chia không hết cho 4 vì 4a ⋮ 4 và 6 không chia hết cho 4
c, Ta có: a b - b a = 10 a + b - 10 b + a = 9a - 9b = 9(a - b) với a > b
Mà 9(a - b) ⋮ 9 nên a b - b a ⋮ 9
d, Ta có: a b c d = 100 a b + c d = 99 a b + a b + c d
Mà 99 a b ⋮ 11 và a b + c d ⋮ 11 (đề bài), nên a b c d ⋮ 11
V
1
10 tháng 9 2015
a chia cho 3 dư 1
=>a=3k+1
b chia cho 3 dư 2
=>a=3k+2
=>a+b=3k+1+3k+2=3k+3=3(k+1) chia hết cho 3
27 tháng 12 2017
achia het cho 2,b chic het cho 2 thi(a+b)chia het cho 2
KV
31 tháng 8 2023
Do a chia 15 dư 2 nên a = 15k + 2 (k ∈ ℕ)
Do b chia 6 dư 1 nên b = 6m + 1 (m ∈ ℕ)
⇒ a + b = 15k + 2 + 6m + 1
= 15k + 6m + 3
= 3.(5k + 2m + 1) ⋮ 3
Vậy (a + b) ⋮ 3
31 tháng 8 2023
\(a:15\) dư 2 => a = 15k + 2 ( k thuộc N
\(a:6\) dư 1 => a = 6k + 1 ( k thuộc N )
=> \(a+b=15k+6k+2+1=21k+3=3\left(7k+1\right)⋮3\)