BM
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
0
S
22 tháng 7 2016
Để phân số trên thỏa mãn điều kiện thì:
3n+4 chia hết cho n-1
3n+4=3n-3+7
=3.(n-1)+7
Vì 3.(n-1) chia hết cho n-1 nên 7 phải chia hết cho n-1
n-1 thuộc +-1;+-7
Thử các trường hợp ra,ta có:
n thuộc:0;2;8;-6.
19 tháng 4 2020
a)Để A là phân số \(\Leftrightarrow n+4\ne0\Leftrightarrow n\ne-4.\)
b) A= \(\frac{3n-5}{n+4}=\frac{3n+12-17}{n+4}=3-\frac{17}{n+4}.\)
A nhận giá trị nguyên <=>\(\frac{17}{n+4}nguyên\)
\(\Rightarrow n+4\inƯ\left(17\right)=\hept{\begin{cases}\\\end{cases}1;-1;17;-17}.\)
\(\Rightarrow n=-3;-5;13;-21\)
học tốt
TB
2
28 tháng 3 2023
Ta có: \(A=\dfrac{3n-4}{3-n}=\dfrac{5-3\left(3-n\right)}{3-n}=\dfrac{5}{3-n}-3\) ( ĐK:\(n\ne3\))
Để \(A\inℤ\) mà \(-3\inℤ\) \(\Rightarrow\dfrac{5}{3-n}\inℤ\)\(\Leftrightarrow3-n\in\text{Ư}\left(5\right)=\left\{1;5;-1;-5\right\}\)
\(\Leftrightarrow n\in\left\{2;-2;4;8\right\}\).
CM
11 tháng 9 2017
Đáp án cần chọn là: B
A = 3 n − 5 n + 4 = 3 n + 12 − 12 − 5 n + 4 = 3 n + 4 + − 17 n + 4 = 3 n + 4 n + 4 + − 17 n + 4 = 3 + − 17 n + 4
Vì n∈Z nên để A∈Z thì n + 4∈U(−17) = {±1;±17}
Ta có bảng:
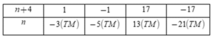
Vậy n∈{−21;−5;−3;13}
AH
Akai Haruma
Giáo viên
4 tháng 2
Lời giải:
Để $A$ nguyên thì:
$3n-5\vdots n+4$
$\Rightarrow 3(n+4)-17\vdots n+4$
$\Rightarrow 17\vdots n+4$
$\Rightarrow n+4\in \left\{\pm 1; \pm 17\right\}$
$\Rightarrow n\in \left\{-3; -5; 13; -21\right\}$
Để \(A\) có giá trị nguyên thì \(\left(3n-5\right)⋮\left(n+4\right)\)
Ta có :
\(3n-5=3n+12-17=3\left(n+4\right)-17\) chia hết cho \(n+4\)\(\Rightarrow\)\(\left(-17\right)⋮\left(n+4\right)\)\(\Rightarrow\)\(\left(n+4\right)\inƯ\left(-17\right)\)
Mà \(Ư\left(-17\right)=\left\{1;-1;17;-17\right\}\)
Suy ra :
Vậy \(n\in\left\{-3;-5;13;-21\right\}\)
A= 3n-5/n+4 = 3(n+4)-17/n+4 (n ≠ -4)
Để A ∈ Z ⇔ 17 chia hết cho n+4 hay n+4 ∈ Ư(17)
⇒ n+4 ∈ {17; -17; 1; -1}
n ∈ {13; -21; -3; -5}
Vậy n ∈ {13; −21; −3; −5}