YT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
4
HT
9 tháng 8 2021
A = 3 + 32 + 33 + ...+3100
3A = 32 + 33 + 34 + ...+ 3101
3A - A = ( 32 + 33 + 34 + ...+ 3101 ) - ( 3 + 32 + 33 + ...+3100 )
2A = 3101 - 3
Thay vào 2A + 3 = 3n ta có
3101 - 3 + 3 = 3n
3101 = 3n
=> n = 101
9 tháng 8 2021
A = 3 + 32 + 33 +....+ 3100
\(\Rightarrow\) 3A= 3.(3 + 32 + 33 +....+ 3100)
\(\Rightarrow\) 3A= 32 + 33 + 34 +.....+ 3101
\(\Rightarrow\)3A - A= (32 + 33 + 34 +.....+ 3101) - (3 + 32 + 33 +....+ 3100)
\(\Rightarrow\)2A= 3101 - 3
mà 2A + 3 = 3n
\(\Rightarrow\)3101 - 3 + 3 = 3n
\(\Rightarrow\)3101 = 3n
\(\Rightarrow\)n=101
NN
4
22 tháng 1 2016
Ta có: 3A=32+33+...+3101
3A-A=2A=(32+33+...+3101)-(3+32+...+3100)
2A=3101-3
A=\(\frac{3^{101}-3}{2}\)
=>2A+3=2.\(\frac{3^{101}-3}{2}\)+3
=(3101-3)+3
=3101
Mà 2A+3=3n
=>3101=3n
=>n=101
22 tháng 1 2016
A=3+32+33+...+3100
2A=(3+32+33+...+3100)x2
2A=32+33+34...+3101
2A-A=3101-3
mà 3n=2A+3=3101-3+3=3101
suy ra n=101
TC
847
11 tháng 6 2021
có A=3+3^2+3^3+..+3^100
3A=3.3+3^2.3+3^3.3+..+3^100.3
3A=3^2+3^3+3^4+..+3^101
⇒2A=(3^2+3^3+3^4+..+3^101)-(3+3^2+3^3+..+3^100)
2A=3^101-3
LẤY 3^101-3+3=3^n
3^101=3^n
⇒n=101
BD
15 tháng 6 2021
Ta có (1)
(2)
Lấy (2) trừ (1) được .
Do đó,
Mà theo đề bài .
Vậy .
D
6
LC
15 tháng 8 2015
=>3A=32+32+…+3101
=>3A-A=32+33+…+3101-3-32-…-3100
=>2A=3101-3
=>2A+3=3101=3N
=>N=101
Vậy N=101
15 tháng 8 2015
3A = \(3^2+3^3+3^4+...+3^{100}+3^{101}\)
\(\Rightarrow3A-A=\left(3^2+3^3+3^4+...+3^{100}+3^{101}\right)\)- \(\left(3+3^2+3^3+..+3^{100}\right)\)
\(\Rightarrow2A=3^{101}-3\Rightarrow2A+3=3^{101}\)
Vậy n = 101
OY
20 tháng 7 2021
A=3+32+33+...+3100
3A=32+33+...+3101
3A-A=(32+33+...+3101)-(3+32+33+...+3100)
2A=3101-3
2A+3=3101
DX
20 tháng 7 2021
\(A=3+3^2+3^3+...+3^{100}\)
\(\Rightarrow3A=3.\left(3+3^2+3^3+...+3^{100}\right)\)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{101}\)
\(\Rightarrow3A-A=2A=\left[3^2+3^3+3^4+...+3^{101}\right]-\left[3+3^2+3^3+...+3^{100}\right]\)\(\Rightarrow2A=3^{101}-3\)
Theo đề bài ta có 2A + 3 = 3n ( \(n\in N\) )
\(\Rightarrow2A+3=3^{101}-3+3=3^n\)
\(\Rightarrow2A+3=3^{101}=3^n\)
\(\Rightarrow3^{101}=3^n\)
\(\Rightarrow101=n\) ( thỏa mãn điều kiện \(n\in N\)
Vậy n = 101
PT
1
CM
22 tháng 11 2018
Ta có: A = 3 + 3 2 + 3 3 + . . . + 3 100
=> 3 A = 3 2 + 3 3 + 3 4 + . . . + 3 101
=> 3 A - A = ( 3 2 + 3 3 + 3 4 + . . . + 3 101 ) - ( 3 + 3 2 + 3 3 + . . . + 3 100 )
=> 2 A = 3 2 + 3 3 + 3 4 + . . . + 3 101 - 3 - 3 2 - 3 3 - . . . - 3 100
2 A = 3 101 - 3 <=> 2 A + 3 = 3 101 , mà 2 A + 3 = 3 n
=> n = 101
TN
2
OY
13 tháng 8 2021
A=3+32+33+...+399
3A=32+33+...+3100
3A-A=(32+33+...+3100)-(3+32+33+...+399)
2A=3100-3
2A+3=3100
⇒n=100
BS
13 tháng 8 2021
Đây nè bạn, chúc bạn học tốt :))
A = 3 + 32 + 33+ ... + 399
3A = 3. (3 + 32 + 33+ ... + 399)
3A \(=3^2+3^3+3^4+...+3^{100}\)
3A \(=\left(3^2+3^3+3^4+...+3^{100}\right)-\left(3+3^2+3^3+...+3^{99}\right)\)
2A\(=3^{100}-3\)
Vậy, sau khi tìm đc 2A, ta tìm stn n nha:
2A + 3 = 3n
\(=3^{100}-3+3=3^n\)
⇒\(3^{100}=3^n\)(Vì -3 +3 = 0)
Vậy n = 100
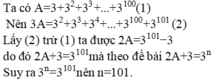
\(3A=3^2+3^3+3^4+...+3^{2021}\)
\(2A=3A-A=3^{2021}-3\)
\(\Rightarrow2A+3=3^{2021}-3+3=3^{2021}=3^n\Rightarrow n=2021\)