Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AB}=\left(3;-3\right)\Rightarrow AB=3\sqrt{2}\)
\(S_{MAB}=\dfrac{1}{2}d\left(M;AB\right).AB=3\Rightarrow D\left(M;AB\right)=\dfrac{6}{AB}=\sqrt{2}\)
Phương trình AB:
\(1\left(x-0\right)+1\left(y-1\right)=0\Leftrightarrow x+y-1=0\)
\(M\in Oy\Rightarrow M\left(0;y\right)\Rightarrow d\left(M;AB\right)=\dfrac{\left|y-1\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
\(\Rightarrow\left|y-1\right|=2\Rightarrow\left[{}\begin{matrix}m=-1\\n=3\end{matrix}\right.\)

Từ giả thiết suy ra \(\overrightarrow{AB}=\left(-2;2\right);\overrightarrow{BC}=\left(4;-3\right)\)
Gọi H(x;y) là trực tâm của tam giác ABC thế thì \(\overrightarrow{CH}=\left(x-2;y\right),\overrightarrow{AH}=\left(x;y-1\right)\)
Ta có H là trực tâm của tam giac ABC khi và chỉ khi
\(\begin{cases}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{CH}.\overrightarrow{AB}=0\end{cases}\)\(\Leftrightarrow\) \(\begin{cases}4x-3\left(y-1\right)=0\\-2\left(x-2\right)+2y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=-9\\y=-11\end{cases}\)
Vậy trực tâm của tam giác ABC là H(-9;-11)
Để tìm tọa độ của tâm I đường tròn ngoại tiếp tam giác ABC ta có thể sử dụng công thức khoảng cách IA=IB=IC hoặc sử dụng đẳng thức Vecto \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{IH}\)
Hoặc cũng có thể làm như sau :
Gọi M và N theo thứ tự là trung điểm của AB và BC. Khi đó M(-1;2) và \(N\left(0;\frac{3}{2}\right)\)
Gọi I(x;y) là tâm đường tròn ngoại tiếp của tam giác. Khi đó :
\(\begin{cases}\overrightarrow{IM}.\overrightarrow{AB}=0\\\overrightarrow{IN}.\overrightarrow{BC}=0\end{cases}\)
\(\Leftrightarrow\begin{cases}-2\left(-1-x\right)+2\left(2-y\right)=0\\4\left(-x\right)-3\left(\frac{3}{2}-y\right)=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\frac{9}{2}\\y=\frac{15}{2}\end{cases}\)
Vậy tâm đường tròn ngoại tiếp của tam giác ABC là \(I\left(\frac{9}{2};\frac{15}{2}\right)\)

H là trực tâm của tam giác nhỉ.
A có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}2x-y+2=0\\x-2y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\Rightarrow A\left(-1;0\right)\)
B có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}2x-y+2=0\\x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\Rightarrow B\left(0;2\right)\)
H có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}x-2y+1=0\\x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\end{matrix}\right.\Rightarrow H\left(0;\dfrac{1}{2}\right)\)
Phương trình đường thẳng AC: \(y=0\)
Phương trình đường thẳng CH: \(x+2y-1=0\)
C có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}y=0\\x+2y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\Rightarrow H\left(1;0\right)\)

ta có : \(M\left(-1;4\right)\) là trung điểm của \(AB\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{x_A+x_B}{2}=-1\\\dfrac{y_A+y_B}{2}=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_A+x_B=-2\\y_A+y_B=8\end{matrix}\right.\).............. (1)
ta có : \(N\left(2;0\right)\) là trung điểm của \(BC\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{x_B+x_C}{2}=2\\\dfrac{y_B+y_C}{2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_B+x_C=4\\y_B+y_C=0\end{matrix}\right.\) ...................(2)
ta có : \(P\left(6;1\right)\) là trung điểm của \(BC\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{x_C+x_A}{2}=6\\\dfrac{y_C+y_A}{2}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_C+x_A=12\\y_C+y_A=2\end{matrix}\right.\)...................(3)
từ : (1) ; (2) và (3) ta có được : hệ phương trình về hoành độ và hệ phương trình về tung độ
phương trình về hoành độ : \(\left\{{}\begin{matrix}x_A+x_B=-2\\x_B+x_C=4\\x_C+x_A=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_A=3\\x_B=-5\\x_C=9\end{matrix}\right.\)...(4)
phương trình về tung độ : \(\left\{{}\begin{matrix}y_A+y_B=8\\y_B+y_C=0\\y_C+y_A=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_A=5\\y_B=3\\y_C=-3\end{matrix}\right.\)........(5)
từ : (4) và (5) ta có được tọa độ điểm : \(A\left(3;5\right)\) ; \(B\left(-5;3\right)\) ; \(C\left(9;-3\right)\)
vậy tọa độ điểm : \(A\left(3;5\right)\) ; \(B\left(-5;3\right)\) ; \(C\left(9;-3\right)\)
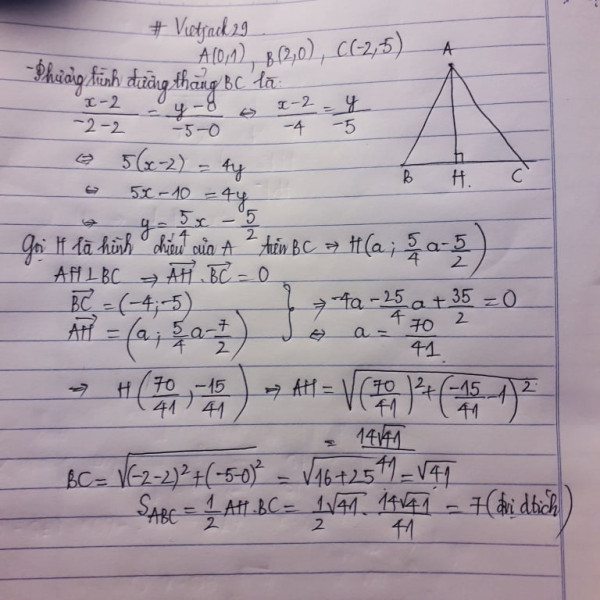
Ừ hứ, lm thế này nà
Có F là giao điểm của BC vs Oy, nên ta sẽ đi tìm pthđ giao điểm của chúng, và nó chính là toạ độ điểm F
\(B,C\in\left(d\right)\Rightarrow\left\{{}\begin{matrix}2a+b=0\\a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-4\\b=8\end{matrix}\right.\Rightarrow y=-4x+8\)
PTHĐGĐ: \(-4.0+8=y=8\) (do thuộc Oy nên x=0)
\(\Rightarrow F\left(0;8\right)\)
Nhìn vào toạ độ của O,F,B thì nhận xét đây là tam giác vuông tại O
\(\Rightarrow S_{\Delta OFB\:}=\frac{OF.OB}{2}=\frac{8.2}{2}=8\left(đvdt\right)\)
Nguyễn Văn Huy uk kcj ^_^