Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ giả thiết suy ra \(\overrightarrow{AB}=\left(-2;2\right);\overrightarrow{BC}=\left(4;-3\right)\)
Gọi H(x;y) là trực tâm của tam giác ABC thế thì \(\overrightarrow{CH}=\left(x-2;y\right),\overrightarrow{AH}=\left(x;y-1\right)\)
Ta có H là trực tâm của tam giac ABC khi và chỉ khi
\(\begin{cases}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{CH}.\overrightarrow{AB}=0\end{cases}\)\(\Leftrightarrow\) \(\begin{cases}4x-3\left(y-1\right)=0\\-2\left(x-2\right)+2y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=-9\\y=-11\end{cases}\)
Vậy trực tâm của tam giác ABC là H(-9;-11)
Để tìm tọa độ của tâm I đường tròn ngoại tiếp tam giác ABC ta có thể sử dụng công thức khoảng cách IA=IB=IC hoặc sử dụng đẳng thức Vecto \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{IH}\)
Hoặc cũng có thể làm như sau :
Gọi M và N theo thứ tự là trung điểm của AB và BC. Khi đó M(-1;2) và \(N\left(0;\frac{3}{2}\right)\)
Gọi I(x;y) là tâm đường tròn ngoại tiếp của tam giác. Khi đó :
\(\begin{cases}\overrightarrow{IM}.\overrightarrow{AB}=0\\\overrightarrow{IN}.\overrightarrow{BC}=0\end{cases}\)
\(\Leftrightarrow\begin{cases}-2\left(-1-x\right)+2\left(2-y\right)=0\\4\left(-x\right)-3\left(\frac{3}{2}-y\right)=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\frac{9}{2}\\y=\frac{15}{2}\end{cases}\)
Vậy tâm đường tròn ngoại tiếp của tam giác ABC là \(I\left(\frac{9}{2};\frac{15}{2}\right)\)

\(p=\dfrac{a+b+c}{2}=15\)
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{15\left(15-8\right)\left(15-10\right)\left(15-12\right)}=15\sqrt{7}\)
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{10^2+12^2-8^2}{2.10.12}=\dfrac{3}{4}\Rightarrow A\approx41^024'\)

Chọn C.
Gọi A’ là chân đường cao kẻ từ A.
Theo câu 64 ta có tọa độ điểm A’ là A’(1;1)
Ta có
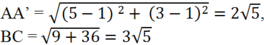
Suy ra ![]()

\(S=\dfrac{1}{2}\left|\left(x_B-x_A\right)\left(y_C-y_A\right)-\left(x_C-x_A\right)\left(y_B-y_A\right)\right|\)
\(=\dfrac{1}{2}\left|\left(2-1\right)\left(-8+5\right)-\left(13-1\right)\left(1+5\right)\right|=\dfrac{75}{2}\)

Chọn B.
Ta có: Nửa chu vi tam giác là: (3 + 4 + 5) : 2 = 6.
Áp dụng công thức Hê rông:
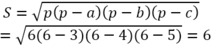

\(a^2=b^2+c^2-2bc.\cos A\Rightarrow a=\sqrt{b^2+c^2-2bc.cosA}=\sqrt{7^2+5^2-\dfrac{2.7.5.3}{5}}=4\sqrt{2}\)
\(\sin A=\sqrt{1-cos^2A}=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
\(p=\dfrac{a+b+c}{2}=6+2\sqrt{2}\)
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=14\)
\(R=\dfrac{a}{2.sinA}=\dfrac{4\sqrt{2}}{\dfrac{2.4}{5}}=\dfrac{5\sqrt{2}}{2}\)
\(r=\dfrac{S}{p}=\dfrac{14}{6+2\sqrt{2}}=3-\sqrt{2}\)
\(ha=\dfrac{2S}{a}=\dfrac{2.14}{4\sqrt{2}}=2\sqrt{2}\)
\(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\)
\(\Leftrightarrow7^2+5^2-a^2=\dfrac{3}{5}\cdot2\cdot7\cdot5=3\cdot2\cdot7=42\)
\(\Leftrightarrow a^2=32\)
hay \(a=4\sqrt{2}\)
\(\sin A=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)

\(AB^2=\left(1+1\right)^2+\left(2-0\right)^2=8\)
\(AC^2=\left(5+1\right)^2+\left(-2-0\right)^2=39\)
\(BC^2=\left(5-1\right)^2+\left(-2-2\right)^2=32\)
Cạnh lớn nhất là AC, ta có:
AC2 < AB2 + BC2
=> Tam giác ABC nhọn
Diện tích ABC= dt(CDEF) - dt(CDB) - dt(CFA) - dt(ABE)
= 5.4 - 4.4/2 - 5.1/2 - 3.1/2
= 8
Gọi H(x,y), ta có BH vuông góc với AC => \(\overrightarrow{BH}.\overrightarrow{AC}=0\) => (x - 1).(5-0) + (y - 2)(-2 +1) = 0
=> 5x - y = 3 (1)
Phương trình đt AC là: \(\frac{y+1}{-2+1}=\frac{x-0}{5-0}\) => 5y + x = -5
Vì H thuộc AC nên 5y + x = -5 (2)
Từ (1) và (2), giải hệ pt ta có: x =5/13 và y = -14/13
Vậy H(5/13; -14/13)
AB2=(1+1)2+(2−0)2=8
AC2=(5+1)2+(−2−0)2=39
BC2=(5−1)2+(−2−2)2=32
Cạnh lớn nhất là AC, ta có:
AC2 < AB2 + BC2
=> Tam giác ABC nhọn
Diện tích ABC= dt(CDEF) - dt(CDB) - dt(CFA) - dt(ABE)
= 5.4 - 4.4/2 - 5.1/2 - 3.1/2
= 8
Gọi H(x,y), ta có BH vuông góc với AC => BH−→−−.AC−→−−=0 => (x - 1).(5-0) + (y - 2)(-2 +1) = 0
=> 5x - y = 3 (1)
Phương trình đt AC là: y+1−2+1=x−05−0 => 5y + x = -5
Vì H thuộc AC nên 5y + x = -5 (2)
Từ (1) và (2), giải hệ pt ta có: x =5/13 và y = -14/13
Vậy H(5/13; -14/13)
REFER
tham khảo