Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A’ là trung điểm của cạnh BC nên -4 = (xB+ xC)
=> xB+ xC = -8 (1)
Tương tự ta có xA+ xC = 4 (2)
xB+ xC = 4 (3)
=> xA+ xB+ xC =0 (4)
Kết hợp (4) và (1) ta có: xA= 8
(4) và (2) ta có: xB= -4
(4) và (3) ta có: xC = -4
Tương tự ta tính được: yA = 1; yB = -5; yC = 7.
Vậy A(8;1), B(-4;-5), C(-4; 7).
Gọi G la trọng tâm tam giác ABC thì
xG= = 0; yG =
= 1 => G(0,1).
xG’= ; yG’ =
= 1 => G'(0;1)
Rõ ràng G và G’ trùng nhau.

Giả sử \(B\left(x;y\right)\).Do \(M\left(2;0\right)\) là trung điểm \(BC\Rightarrow C\left(4-x;-y\right)\).
Do \(N\left(2;3\right)\) là trung điểm \(CA\) \(\Rightarrow A\left(x;6+y\right)\)
Do \(P\left(-1;3\right)\) là trung điểm \(AB\Rightarrow\left\{{}\begin{matrix}x+x=2.\left(-1\right)\\6+y+y=2.3\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2x=-2\\2y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\\ \Rightarrow B\left(-1;0\right);A\left(-1;6\right);C\left(5;0\right)\).

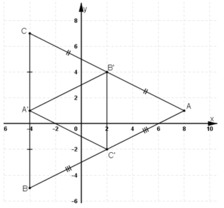
A’ là trung điểm của BC 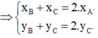
B’ là trung điểm của AC 
C’ là trung điểm của BA 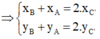
Gọi G là trọng tâm ΔABC và G’ là trọng tâm ΔA’B’C’
Ta có :
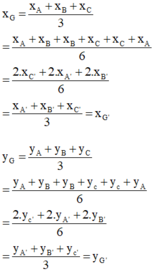
Vậy G ≡ G’ (đpcm)

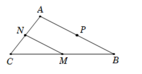
Từ giả thiết suy ra
\(\overrightarrow{MN}=\left(-7;1\right);\overrightarrow{MP}=\left(-3;4\right)\) và tứ giá MNAP là hình bình hành nên \(\overrightarrow{OA}=\overrightarrow{ON}+\overrightarrow{OP}-\overrightarrow{OM}\)
Suy ra A(-4;3)
Do N là trung điểm CA và P là trung điểm AB nên \(\overrightarrow{OC}=2\overrightarrow{ON}-\overrightarrow{OA}\) và \(\overrightarrow{OB}=2\overrightarrow{OP}-\overrightarrow{OA}\)
Suy ra B(10;1) và C(2;5)
ta có : \(M\left(-1;4\right)\) là trung điểm của \(AB\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{x_A+x_B}{2}=-1\\\dfrac{y_A+y_B}{2}=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_A+x_B=-2\\y_A+y_B=8\end{matrix}\right.\).............. (1)
ta có : \(N\left(2;0\right)\) là trung điểm của \(BC\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{x_B+x_C}{2}=2\\\dfrac{y_B+y_C}{2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_B+x_C=4\\y_B+y_C=0\end{matrix}\right.\) ...................(2)
ta có : \(P\left(6;1\right)\) là trung điểm của \(BC\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{x_C+x_A}{2}=6\\\dfrac{y_C+y_A}{2}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_C+x_A=12\\y_C+y_A=2\end{matrix}\right.\)...................(3)
từ : (1) ; (2) và (3) ta có được : hệ phương trình về hoành độ và hệ phương trình về tung độ
phương trình về hoành độ : \(\left\{{}\begin{matrix}x_A+x_B=-2\\x_B+x_C=4\\x_C+x_A=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_A=3\\x_B=-5\\x_C=9\end{matrix}\right.\)...(4)
phương trình về tung độ : \(\left\{{}\begin{matrix}y_A+y_B=8\\y_B+y_C=0\\y_C+y_A=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_A=5\\y_B=3\\y_C=-3\end{matrix}\right.\)........(5)
từ : (4) và (5) ta có được tọa độ điểm : \(A\left(3;5\right)\) ; \(B\left(-5;3\right)\) ; \(C\left(9;-3\right)\)
vậy tọa độ điểm : \(A\left(3;5\right)\) ; \(B\left(-5;3\right)\) ; \(C\left(9;-3\right)\)