
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

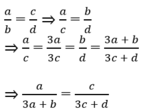

\(\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{d}=\dfrac{a}{d}\) ; \(\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{d}=\dfrac{a}{b}.\dfrac{a}{b}.\dfrac{a}{b}=\dfrac{a^3}{b^3}\)
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b+c}{b+c+d}\)
\(\Rightarrow\dfrac{a^3}{b^3}=\dfrac{\left(a+b+c\right)^3}{\left(b+c+d\right)^3}=\dfrac{a}{d}\).

Lê Minh Tuấn bn tham khảo nha:
a+b+c+d=0
=>a+b=-(c+d)
=> (a+b)^3=-(c+d)^3
=> a^3+b^3+3ab(a+b)=-c^3-d^3-3cd(c+d)
=> a^3+b^3+c^3+d^3=-3ab(a+b)-3cd(c+d)
=> a^3+b^3+c^3+d^3=3ab(c+d)-3cd(c+d) ( vi a+b = - (c+d))
==> a^3 +b^^3+c^3+d^3==3(c+d)(ab-cd) (dpcm)

Do a/b=c/d ⇔ ad=bc
1) Ta có: (a+c)b=ab+bc
(b+d)a=ab+ad
Do bc=ad nên ab+ad=ab+bc
Suy ra (a+c)b=(b+d)a (đpcm)
2) Ta có: (b+d)c=bc+dc
(a+c)d=ad+cd
Do bc=ad nên bc+dc=ad+cd
Suy ra (b+d)c=(b+d)c (đpcm)
3)Ta có:(a+b)(c-d)=ac-ad+bc-bd=(ac-bd)-(ad-bc)
(a-b)(c+d)=ac+ad-bc-bd=(ac-bd)+(ad-bc)
Do ad=bc ⇔ ad-bc=0 nên (ac-bd)-(ad-bc)=(ac-bd)+(ad-bc)
⇔(a+b)(c-d)= (a-b)(c+d) (đpcm)

Đặt \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\b=ck\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^3+b^3+c^3}{b^3+c^3+d^3}=\dfrac{b^3k^3+c^3k^3+d^3k^3}{b^3+c^3+d^3}=k^3\)
\(\dfrac{a}{d}=\dfrac{bk}{d}=\dfrac{ck^2}{d}=\dfrac{dk^3}{d}=k^3\)
Do đó: \(\dfrac{a^3+b^3+c^3}{b^3+c^3+d^3}=\dfrac{a}{d}\)

Ta có: a/b=c/d => a/c=b/d=(a-b)/(c-d)
=> (a-b)3/(c-d)3=a3/c3 (1)
Mặt khác: a/c=b/d =>a3/c3=b3/d3=(a3+b3)/(c3+d3) (2)
Từ (1) và (2) => đccm

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:\(\left(\dfrac{a+b}{c+d}\right)^3=\left(\dfrac{bk+b}{dk+d}\right)^3=\left(\dfrac{b.\left(k+1\right)}{d.\left(k+1\right)}\right)^3=\dfrac{b^3}{d^3}\)(1)
Lại có :\(\dfrac{a^3+b^3}{c^3+d^3}=\dfrac{b^3k^3+b^3}{d^3k^3+d^3}=\dfrac{b^3.\left(k^3+1\right)}{d^3.\left(k^3+1\right)}=\dfrac{b^3}{d^3}\)(2)
Từ (1) và (2) => ĐPCM
Từ a/b=c/d
=>a/c=b/d=a+b/c+d
<=>a^3/c^3=b^3/d^3=(a+b)^3(c+d)^3
=a^3+b^3/c^3+d^3
Vậy
(a+b)^3(c+d)^3=a^3+b^3/c^3+d^3 (đpcm)



Ta có :
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\)
Áp dụng t/c dãy tỉ số bawg nhau ta có :
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b+c}{b+c+d}\)
\(\Leftrightarrow\left(\dfrac{a}{b}\right)^3=\left(\dfrac{b}{c}\right)^3=\left(\dfrac{c}{d}\right)^3=\left(\dfrac{a+b+c}{b+c+d}\right)^3=\dfrac{a}{b}.\dfrac{a}{b}.\dfrac{a}{b}=\dfrac{b}{c}.\dfrac{b}{c}.\dfrac{b}{c}=\dfrac{c}{d}.\dfrac{c}{d}.\dfrac{c}{d}=\dfrac{a}{d}\)
\(\Leftrightarrow\left(\dfrac{a+b+c}{b+c+d}\right)^3=\dfrac{a}{d}\left(đpcm\right)\)