
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=>4a^2-5ab+b^2=0
=>(a-b)(4a-b)=0
=>a=b hoặc b=4a(loại)
=>P=b^2/3b^2=1/3

Ta có:
\(4a^2+b^2=5ab\Leftrightarrow4a^2+b^2-4ab-ab=0\)
\(\Leftrightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\Leftrightarrow\left(a-b\right)\left(4a-b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-b=0\\4a-b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=b\left(ktm\right)\\4a=b\left(tm\right)\end{matrix}\right.\)
\(\Rightarrow4a=b\)
\(\Rightarrow\dfrac{5ab}{3a^2+2b^2}=\dfrac{5a.4a}{3a^2+2.\left(4a\right)^2}=\dfrac{20a^2}{3a^2+32a^2}\)
\(=\dfrac{20a^2}{35a^2}=\dfrac{4}{7}\)
\(4a^2+b^2=5ab\)
\(\Rightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\Rightarrow\left(a-b\right)\left(4a-b\right)=0\)
\(\Rightarrow b=4a\left(do.a\ne b\right)\)
\(\dfrac{5ab}{3a^2+2b^2}=\dfrac{20a^2}{3a^2+32a^2}=\dfrac{4}{7}\)

\(4a^2+b^2=5ab\)
\(4a^2-5ab+b^2=0\)
\(4a^2-4ab-ab+b^2=0\)
\(4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\left(a-b\right)\left(4a-b\right)=0\)
\(\left[\begin{array}{nghiempt}a-b=0\\4a-b=0\end{array}\right.\)
\(\left[\begin{array}{nghiempt}a=b\\4a=b\end{array}\right.\)
mà \(2a>b>0\)
\(\Rightarrow a=b\)
Thay a = b vào M, ta có:
\(M=\frac{b\times b}{4b^2-b^2}\)
\(=\frac{b^2}{3b^2}\)
\(=\frac{1}{3}\)
Vậy . . .

Ta có
\(4a^2+b^2=5ab\Leftrightarrow\left(4a^2-4ab\right)+\left(b^2-ab\right)=0\)
\(\Leftrightarrow\left(a-b\right)\left(4a-b\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}b=a\\b=4a\end{cases}}\)
Thế b = a vào M ta được
\(M=\frac{a.a}{4a^2-a^2}=\frac{1}{3}\)
Thế b = 4a vào M được
\(M=\frac{a.4a}{4a^2-16a^2}=-\frac{1}{3}\)

Theo đề bài ta có :
\(4a^2+b^2=5ab\)
\(\Rightarrow4a^2-4ab-ab+b^2=0\)
\(\Rightarrow\left(a-b\right)\left(4a-b\right)=0\)(1)
Vì \(2a>b>0\)
\(\Rightarrow4a-b\ne0\)
Từ điều (1)
\(\Rightarrow a-b=0\)
\(\Leftrightarrow a=b\)
Thay a=b vào P ta có :
\(P=\frac{ab}{4a^2-b^2}=\frac{a^2}{4a^2-a^2}=\frac{1}{3}\)( vì \(a\ne0\))
Vậy phân thức P có số trị là 1/3 .

Từ \(4a^2+b^2=5ab,\)ta có : \(4a^2-4ab-ab+b^2=0\)
Hay \(\left(a-b\right)\left(4a-b\right)=0\left(.\right)\)
Vì \(2a>b>0\) nên \(4a-b\ne0.\)
Từ \(\left(.\right)\Rightarrow a-b=0\). Tức là \(a=b.\)
Thay \(a=b\) vào \(P\) ta được :
\(P=\frac{ab}{4a^2-b^2}=\frac{a^2}{4a^2-a^2}=\frac{1}{3}\) ( do \(a\ne0\)).

Từ \(4a^2+b^2=5ab\Rightarrow4a^2+b^2-5ab=0\)
\(\Rightarrow4a^2-ab-4ab+b^2=0\)
\(\Rightarrow a\left(4a-b\right)-b\left(4a-b\right)=0\)
\(\Rightarrow\left(a-b\right)\left(4a-b\right)=0\)
\(\Rightarrow\orbr{\begin{cases}a-b=0\\4a-b=0\end{cases}\Rightarrow}\orbr{\begin{cases}a=b\\a=\frac{b}{4}\end{cases}}\)
*)Xét \(a=b\) thì \(F=\frac{b^2}{4b^2-b^2}=\frac{b^2}{3b^2}=\frac{1}{3}\)
*)Xét \(a=\frac{b}{4}\) thì \(F=\frac{\frac{b^2}{4}}{\frac{b^2}{4}-b^2}=-\frac{1}{3}\)
Ta thấy A gồm có 99 số hạng nên ta nhóm mỗi nhóm 3 số hạng.
Ta có: A = 1 + 5 + 52 + 53 + 54 + 55 +...+ 597 + 598 + 599
= (1 + 5 + 52 )+ (53 + 54 + 55 )+...+( 597 + 598 + 599 )
=(1 + 5 + 52 )+ 53(1 + 5 + 52 ) +...+ 597(1 + 5 + 52 )
= ( 1 + 5 + 52)(1 + 53+....+597)
= 31(1 + 53+....+597)
Vì có một thừa số là 31 nên A chia hết cho 31.
P/s Đừng để ý câu trả lời của mình

Ta có : \(4a^2+b^2=5ab\Leftrightarrow4a^2-5ab+b^2=0\Leftrightarrow4a^2-4ab-ab+b^2=0\)
\(\Leftrightarrow4a\left(a-b\right)-b\left(a-b\right)=0\Leftrightarrow\left(4a-b\right)\left(a-b\right)=0\)(1)
Ta thấy \(2a>b>0\left(gt\right)\) nên \(4a>b>0\Rightarrow4a-b>0\)
Từ đó để (1) xảy ra \(\Leftrightarrow a-b=0\Leftrightarrow a=b\) Thay vào P ta được :
\(P=\frac{ab}{4a^2-b^2}=\frac{a.a}{4a^2-a^2}=\frac{a^2}{3a^2}=\frac{1}{3}\)
Vậy \(P=\frac{1}{3}\)
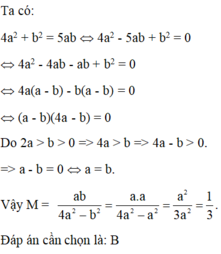
Từ \(4a^2+b^2=5ab\) suy ra \(4a^2-4ab-ab+b^2=0\)
Hay \(4a\left(a-b\right)-b\left(a-b\right)=0\) \(\Leftrightarrow\) \(\left(a-b\right)\left(4a-b\right)=0\) \(\left(\text{*}\right)\)
Vì \(2a>b>0\) nên \(4a-b\ne0\)
Do đó, từ \(\left(\text{*}\right)\) ta suy ra \(a-b=0\) , tức là \(a=b\)
Thay \(a=b\) vào \(P\) , ta được: \(P=\frac{ab}{4a^2-b^2}=\frac{a^2}{4a^2-a^2}=\frac{1}{3}\) (do \(a\ne0\) )