
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2x^2+5x=12\)
\(\Leftrightarrow2x^2+5x-12=0\)
\(\Leftrightarrow2x^2+8x-3x-12=0\)
\(\Leftrightarrow2x\left(x+4\right)-3\left(x+4\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x+4=0\\2x-3=0\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-4\\x=\frac{3}{2}\end{array}\right.\)
Vậy ............

\(2x^2+5x=12\)
\(\Leftrightarrow2x^2+5x-12=0\)
\(\Leftrightarrow2x^2+8x-3x-12=0\) .
\(\Leftrightarrow2x\left(x+4\right)-3\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\2x-3=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-4\\x=\frac{3}{2}\end{cases}}\)

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{2x+3y-z-2-6+3}{2\cdot2+3\cdot3-4}=5\)
Do đó: x-1=10; y-2=15; z-3=20
=>x=11; y=17; z=23
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
Do đó: x=18; y=16; z=15
c: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{2}\\\dfrac{y}{5}=\dfrac{z}{7}\end{matrix}\right.\Leftrightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{14}\)
Trường hợp 1: 2x-3y+5z=-1
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{14}=\dfrac{2x-3y+5z}{2\cdot15-3\cdot10+5\cdot14}=\dfrac{-1}{70}\)
Do đó: x=-15/70=-3/14; y=-10/70=-1/7; z=-14/70=-1/5
Trường hợp 2: 2x-3y+5z=1
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{14}=\dfrac{2x-3y+5z}{2\cdot15-3\cdot10+5\cdot14}=\dfrac{1}{70}\)
Do đó: x=15/70=3/14; y=1/7; z=1/5

\(P=2x^2y+2xy^2-2xy+5\)
\(P=2xy\left(x+y-1\right)+5\)
Thay x + y = 1 ta có :
\(P=2xy\left(1-1\right)+5\)
\(P=2xy\cdot0+5\)
\(P=5\)
Vậy....

TH1:x+y+z=0
\(\Rightarrow\left\{\begin{matrix}x+y=-z\\y+z=-x\\x+z=-y\end{matrix}\right.\)
\(\Rightarrow M=\frac{\left(x+y\right)\left(y+z\right)\left(z+x\right)}{8xyz}=\frac{-xyz}{8xyz}=\frac{-1}{8}\)
TH2: \(x+y+z\ne0\)
Ta có:
\(\frac{2x+2y-z}{z}=\frac{2x-y+2z}{y}=\frac{-x+2y+2z}{x}\)
\(\Rightarrow\left(\frac{2x+2y-z}{z}+3\right)=\left(\frac{2x-y+2z}{y}+3\right)=\left(\frac{-x+2y+2z}{x}+3\right)\)\(\Rightarrow\frac{2x+2y+z}{z}=\frac{2x+2y++2z}{y}=\frac{2x+2y+2z}{x}\)
\(\Rightarrow x=y=z\)
\(\Rightarrow M=\frac{\left(x+y\right)\left(y+z\right)\left(z+x\right)}{8xyz}=\frac{2x.2y.2z}{8xyz}=1\)
Vậy M=1 hoặc M=\(\frac{-1}{8}\)
theo bài ra ta có:
\(\frac{2x+2y-z}{z}=\frac{2x-y+2z}{y}=\frac{-x+2y+2z}{x}\)
\(\Rightarrow\frac{2x+2y-z}{x}+3=\frac{2x-y+2z}{y}+3=\frac{2y+2z-x}{x}+3\)
\(\Rightarrow\frac{2x+2y+2z}{z}=\frac{2x+2z+2y}{y}=\frac{2y+2z+2x}{x}\)
vì x;y;z là các số hữu tỉ khác 0
=> x = y = z
vậy ta có:
\(M=\frac{\left(x+y\right)\left(y+z\right)\left(z+x\right)}{8xyz}=\frac{2x.2y.2z}{8xyz}=\frac{8xyz}{8xyz}=1\)
vậy M = 1
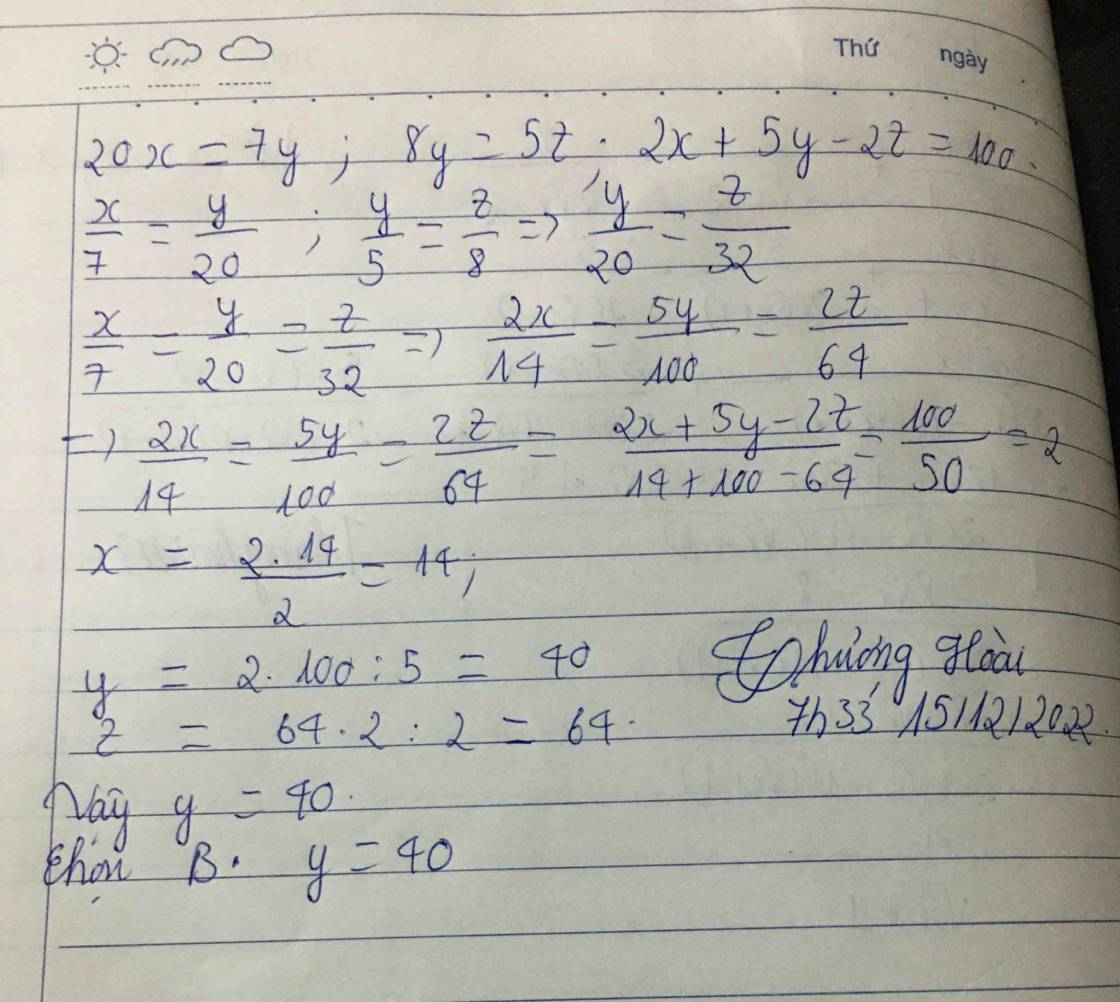
Ta có: 2x + y = 40
=> y = 40 - 2x
Thay y = 40 - 2x vào 2x - y = 12 ta được:
2x - ( 40 - 2x ) = 12
2x - 40 + 2x = 12
( 2x + 2x ) - 40 = 12
4x - 40 = 12
4x = 12 + 40
4x = 52
=> x = 13
Thay x = 13 vào 2x + y = 40 ta được:
2 . 13 + y = 40
=> 26 + y = 40
=> y = 14
Vậy y = 14
# Học tốt #
^O^
#HOK TỐT NHA BẠN#
Đặt 2x = z
Khi đó : 2x + y = z + y = 40 (1)
2x - y = z - y = 12 (2)
Từ (1) và (2) => z > y
=> z = (40 + 12) : 2 = 26 => x = 26 : 2 = 13
=> y = (40 - 12) : 2 = 14
Vậy x = 13 ; y = 14