
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\) ; \(\forall a;b;c\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Rightarrow ab+bc+ca\le1\)
\(\Rightarrow P_{max}=1\) khi \(a=b=c\)
Lại có:
\(\left(a+b+c\right)^2\ge0\) ; \(\forall a;b;c\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)\ge0\)
\(\Leftrightarrow ab+bc+ca\ge-\dfrac{a^2+b^2+c^2}{2}=-\dfrac{1}{2}\)
\(P_{min}=-\dfrac{1}{2}\) khi \(a+b+c=0\)

1: (a-1)(a-3)(a-4)(a-6)+9
=(a^2-7a+6)(a^2-7a+12)+9
=(a^2-7a)^2+18(a^2-7a)+81
=(a^2-7a+9)^2>=0
b: \(A=\dfrac{a^4-4a^3+a^2+4a^3-16a+4+16a-3}{a^2}=\dfrac{16a-3}{a^2}\)
a^2-4a+1=0
=>a=2+căn 3 hoặc a=2-căn 3
=>A=11-4căn 3 hoặc a=11+4căn 3

Lời giải:
$a^2+b^2+c^2-ab-bc-ac=0$
$\Leftrightarrow 2a^2+2b^2+2c^2-2ab-2bc-2ac=0$
$\Leftrightarrow (a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ac+a^2)=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
Vì $(a-b)^2; (b-c)^2; (c-a)^2\geq 0$ với mọi $a,b,c$ nên để tổng của chúng bằng $0$ thì:
$a-b=b-c=c-a=0$
$\Rightarrow a=b=c$
$\Rightarrow \frac{a}{b}=\frac{b}{c}=\frac{c}{a}=1$
Khi đó:
$(\frac{a}{b}+1)(\frac{b}{c}+1)(\frac{c}{a}+1)=(1+1)(1+1)(1+1)=8$
Ta có đpcm.

\(\left(ad+bc\right)\left(a^2d^2+b^2c^2\right)=0\)
\(\Rightarrow a^3d^3+adb^2c^2+bca^2d^2+b^3c^3=0\)
\(\Rightarrow a^3d^3+abcd\left(bc+ad\right)+b^3c^3=0\)
\(\Rightarrow a^3d^3+abcd.0+b^3c^3=0\)
\(\Rightarrow a^3d^3+b^3c^3=0\)
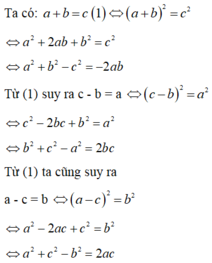


\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}=-\frac{1}{c}\)
\(\Leftrightarrow\left(\frac{1}{a}+\frac{1}{b}\right)^3=\left(-\frac{1}{c}\right)^3\)
\(\Leftrightarrow\frac{1}{a^3}+\frac{3}{a^2b}+\frac{3}{ab^2}+\frac{1}{b^3}=-\frac{1}{c^3}\)
\(\Leftrightarrow\frac{1}{a^3}+\frac{3}{ab}\left(\frac{1}{a}+\frac{1}{b}\right)+\frac{1}{b^3}=-\frac{1}{c^3}\)
\(\Leftrightarrow\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{-3}{ab}\left(\frac{1}{a}+\frac{1}{b}\right)=\frac{-3}{ab}\cdot\frac{-1}{c}=\frac{3}{abc}\)
Ta có: \(M=\frac{bc}{a^2}+\frac{ca}{b^2}+\frac{ab}{c^2}=\frac{abc}{a^3}+\frac{abc}{b^3}+\frac{abc}{c^3}=abc\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)=abc\cdot\frac{3}{abc}=3\)