Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi 3 phần lần lượt là a, b, c.
Theo đề bài ta có: \(0,2a=\dfrac{10}{3}b=\dfrac{4}{5}c\)
\(\Rightarrow\dfrac{1}{5}a=\dfrac{10}{3}b=\dfrac{4}{5}c\)
\(\Rightarrow\dfrac{a}{5}=\dfrac{10b}{3}=\dfrac{4c}{5}\)
\(\Rightarrow\dfrac{a}{5}.15=\dfrac{10b}{3}.15=\dfrac{4c}{5}.15\)
\(\Rightarrow3a=50b=12c\)
\(\Rightarrow\dfrac{3a}{300}=\dfrac{50b}{300}=\dfrac{12c}{300}\)
\(\Rightarrow\dfrac{a}{100}=\dfrac{b}{6}=\dfrac{c}{25}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{100}=\dfrac{b}{6}=\dfrac{c}{25}=\dfrac{a+b+c}{100+6+25}=\dfrac{786}{131}=6\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{100}=6\Rightarrow a=6.100=600\\\dfrac{b}{6}=6\Rightarrow b=6.6=36\\\dfrac{c}{25}=6\Rightarrow c=6.25=150\end{matrix}\right.\)
Vậy chia số 786 thành 3 phần là 600 ; 36 ; 150
Gọi hệ số tỉ lệ của x và y là a, nghĩa là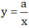 
hay x.y = a.
Ta có x = 4 thì y = 1,5 nên suy ra a = x.y = 4.1,5 = 6.
Vậy x.y = 6.
Khi x = 0,5 thì y = 6 : 0,5 = 12.
Khi x = -1,2 thì y = 6 : (-1,2) = -5
Khi y = 3 thì x = 6 : 3 =2
Khi y = -2 thì x = 6 : (-2) = -3.
Khi x = 6 thì y = 6 : 6 = 1.
Vậy ta có bảng sau :
| x | 0,5 | -1,2 | 2 | -3 | 4 | 6 |
| y | 12 | -5 | 3 | -2 | 1,5 | 1 |
2, Ta có: f(5)= 2.5=10
3, Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ là 3 thì: y= 3x
4, ... x thì tỉ lệ nghịch với y theo hệ số tỉ lệ là: a
5, .... Ta có: xy= 60 hay x và y tỉ lệ nghịch theo hệ số tỉ lệ là: 60
6, Tọa độ của góc O trong mặt phẳng tọa độ là: (0;0)
Answer:
Câu 1:
Gọi ba phần được chia từ số 470 lần lượt là x, y, z
Có: Ba phần tỉ lệ nghịch với 3, 4, 5
\(\Rightarrow x3=y4=z5\Rightarrow\frac{x}{20}=\frac{y}{15}=\frac{z}{12}\) và \(x+y+z=470\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{x}{20}=\frac{y}{15}=\frac{z}{12}=\frac{x+y+z}{20+15+12}=\frac{470}{47}=10\)
\(\Rightarrow\hept{\begin{cases}x=200\\y=150\\z=120\end{cases}}\)
Câu 2:
Gọi ba phần được chia từ số 555 lần lượt là x, y, z
\(\Rightarrow\hept{\begin{cases}x+y+z=55\\4x=5y=6z\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x+y+z=55\\\frac{x}{15}=\frac{y}{12}=\frac{z}{10}=\frac{x}{15+12+10}=\frac{555}{35}=\frac{111}{7}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{1665}{7}\\y=\frac{1332}{7}\\z=\frac{1110}{7}\end{cases}}\)
Câu 3:
Gọi ba phần được chia từ số 314 lần lượt là x, y, z
\(\Rightarrow\hept{\begin{cases}x+y+z=314\\\frac{2}{3}x=\frac{2}{5}y=\frac{3}{7}z\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x+y+z=314\\\frac{2x}{3}=\frac{2y}{5}=\frac{3z}{7}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x+y+z=314\\\frac{x}{9}=\frac{y}{15}=\frac{z}{14}=\frac{x+y+z}{9+15+14}=\frac{314}{38}=\frac{157}{19}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{1413}{19}\\y=\frac{2355}{19}\\z=\frac{2198}{19}\end{cases}}\)
Gọi 4 số cần tìm lần lượt là a, b, c, d (a, b, c, d \(\ne0\) )
Theo đề ta có: \(\dfrac{5}{9}a=0,5b=\dfrac{2}{9}c=1,5d\)
\(\Rightarrow\dfrac{5a}{9}=\dfrac{b}{2}=\dfrac{2c}{9}=\dfrac{3d}{2}\)
\(\Rightarrow\dfrac{a}{\dfrac{9}{5}}=\dfrac{b}{2}=\dfrac{c}{\dfrac{9}{2}}=\dfrac{d}{\dfrac{2}{3}}\)
và a + b + c + d = 2690
Áp dụng t/c của dãy tỉ số = nhau ta có:
\(\dfrac{a}{\dfrac{9}{5}}=\dfrac{b}{2}=\dfrac{c}{\dfrac{9}{2}}=\dfrac{d}{\dfrac{2}{3}}=\dfrac{a+b+c+d}{\dfrac{9}{5}+2+\dfrac{9}{2}+\dfrac{2}{3}}=\dfrac{2690}{\dfrac{269}{30}}=300\)
\(\Rightarrow\left[{}\begin{matrix}a=300\cdot\dfrac{9}{5}\\b=300\cdot2\\c=300\cdot\dfrac{9}{2}\\d=300\cdot\dfrac{2}{3}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}a=540\\b=600\\c=1350\\d=200\end{matrix}\right.\)
Vậy 4 số cần tìm là .............................