Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

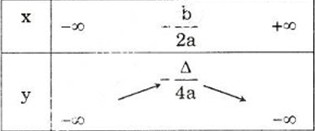
Nếu \(a>0\) thì hàm số \(y=ax^2+bx+c\)
Nghịch biến trên khoảng: \(\left(-\infty;-\dfrac{b}{2a}\right)\);
Đồng biến trên khoảng: \(\left(\dfrac{-b}{2a};+\infty\right)\).
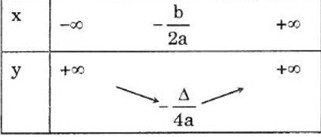
Nếu \(a< 0\) thì hàm số \(y=ax^2+bx+c\):
Nghịch biến trên khoảng: \(\left(\dfrac{-b}{2a};+\infty\right)\);
Đồng biến trên khoảng: \(\left(-\infty;-\dfrac{b}{2a}\right)\).

Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)

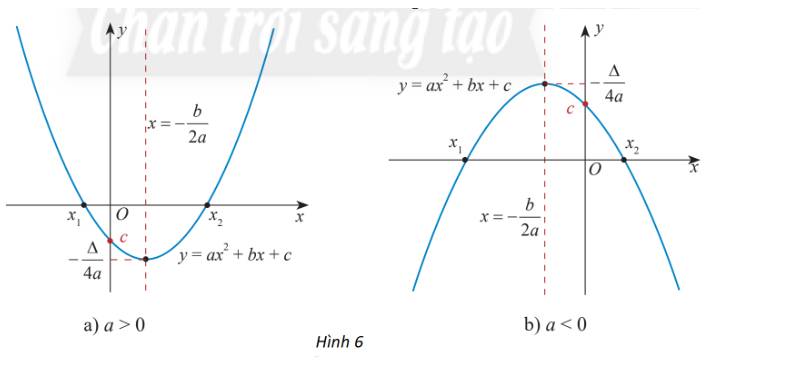
a)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \frac{b}{{2a}}; + \infty )\), khoảng nghịch biến là \(( - \infty ; - \frac{b}{{2a}})\)
b)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \infty ; - \frac{b}{{2a}})\), khoảng nghịch biến là \(( - \frac{b}{{2a}}; + \infty )\)


Nhìn vào đồ thị, ta thấy:
a) Hàm số \(y = - 2x + 1\)nghịch biến trên \(\mathbb{R}\)
b) Hàm số \(y = - \frac{1}{2}{x^2}\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\); nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)

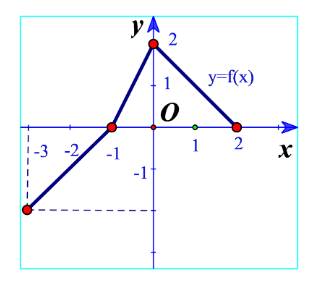
Từ đồ thị hàm số ta thấy khi x tăng từ -3 đến -1 và từ -1 đến 0 thì đồ thị đi lên nên hàm số đồng biến trên các khoảng (-3;-1) và (-1;0).
Khi x tăng từ 0 đến 2 thì đồ thị đi xuống nên hàm số nghịch biến trên (0;2).

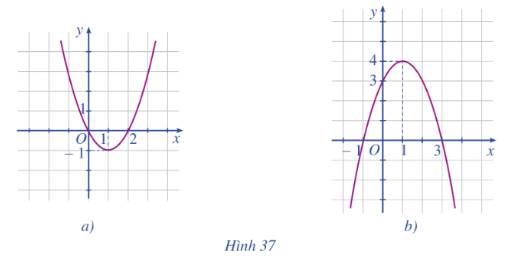
a)
Hình 37a: Bề lõm hướng lên trên nên a>0
Hình 37b: Bề lõm xuống nên a<0
b)
Hình 37a: Đỉnh là (1;-1), trục đối xứng x=1
Hình 37b: Đỉnh là (1;4), trục đối xứng x=1
c)
Hình 37a: Hàm số đồng biến trên \(\left( {1; + \infty } \right)\)
Hình 37b: Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\)
d)
Hình 37a: Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\)
Hình 37b: Hàm số nghịch biến trên \(\left( {1; + \infty } \right)\)
e)
Hình 37a: Đồ thị nằm trên trục Ox khi \(x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
=> Khoảng giá trị x mà y > 0 là \(\left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
Hình 37b: Đồ thị nằm trên trục Ox khi \(x \in \left( { - 1;3} \right)\)
=> Khoảng giá trị x mà y > 0 là \(\left( { - 1;3} \right)\)
g)
Hình 37a: Đồ thị nằm dưới trục Ox khi \(x \in \left[ {0;2} \right]\)
=> Khoảng giá trị x mà y < 0 là \(\left[ {0;2} \right]\)
Hình 37b: Đồ thị nằm dưới trục Ox khi \(x \in \left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)
=> Khoảng giá trị x mà \(y \le 0\) là \(\left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)

- Khi a > 0, hàm số y = ax + b đồng biến trên khoảng (-∞; +∞) hay đồng biến trên R.
- Khi a < 0, hàm số y = ax + b nghịch biến trên khoảng (-∞; +∞) hay nghịch biến trên R.