Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

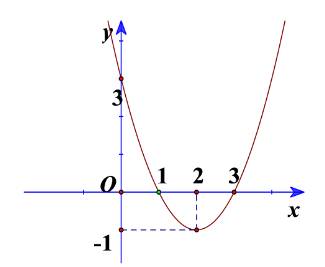
a) Trục đối xứng là đường thẳng \(x = 2\)
Đỉnh là \(I\left( {2; - 1} \right)\)
b) Từ đồ thị ta thấy trên khoảng \(\left( { - \infty ;2} \right)\) thì hàm số đi xuống nên hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\).
Trên khoảng \(\left( {2; + \infty } \right)\) thì hàm số đi xuống nên đồng biến trên \(\left( {2; + \infty } \right)\).
c) ) Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Đồ thị hàm số có đỉnh là \(I\left( {2; - 1} \right)\) nên ta có:
\(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\a{.2^2} + b.2 + c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2b + c = - 1\end{array} \right.\)
Ta lại có điểm \(\left( {1;0} \right)\) thuộc đồ thị nên ta có: \(a + b + c = 0\)
Vậy ta có hệ sau:
\(\left\{ \begin{array}{l}b = - 4a\\4a + 2b + c = - 1\\a + b + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2.\left( { - 4a} \right) + c = - 1\\a + \left( { - 4a} \right) + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\c - 4a = - 1\\c - 3a = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\a = 1\\c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4\\a = 1\\c = 3\end{array} \right.\)
Vậy parabol là \(y = {x^2} - 4x + 3\)

a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
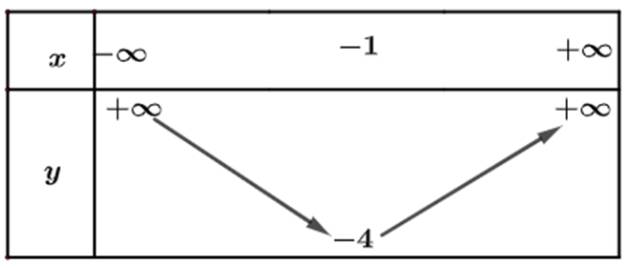
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
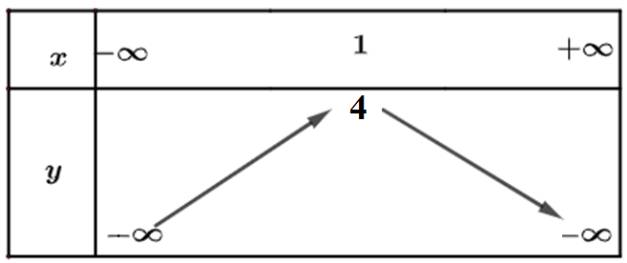

Kết quả của mỗi lần thử là một cặp (i; j) với i và j lần lượt là số chấm xuất hiện trên hai xúc xắc, hai con xúc xắc gieo đồng thời nên không quan tâm thứ tự, ta có không gian mẫu là:
\(\Omega = \begin{array}{l}\{(1;1),(1;2),(1;3),(1;4),(1;5),(1;6),(2;2),(2;3),(2;4),(2;5),(2;6),(3;3),(3;4),(3;5),(3;6),\\(4;4),(4;5),(4;6),(5;5),(5;6),(6;6)\}\end{array} \)
Không gian mẫu gồm có 21 kết quả, tức là \(n\left( \Omega \right) = 21\)
a) Ta có tập hợp miêu tả biến cố A
\(A = \left\{ {(1;1),(2;2),(3;3),(4;4),(5;5),(6;6)} \right\} \Rightarrow n\left( A \right) = 6\)
Do đó, xác suất của biến cố A là: \(P\left( A \right) = \frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{21}} = \frac{2}{7}\)
b) Ta có tập hợp miêu tả biến cố B
\(B = \left\{ {(6;3),(5;4)} \right\} \Rightarrow n\left( B \right) = 2\)
Do đó, xác suất của biến cố B là: \(P\left( B \right) = \frac{{n(B)}}{{n(\Omega )}} = \frac{2}{{21}}\)

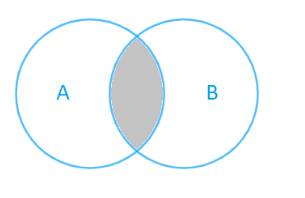
Phần màu xám là phần giao nhau giữa tập hợp A và tập hợp B: vừa thuộc A, vừa thuộc B.
Do đó phần màu xám là \(A \cap B\)
Chọn đáp án A

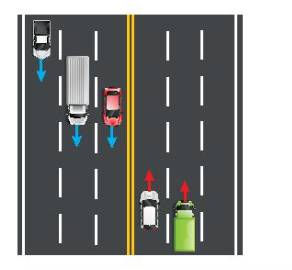
a) Các làn đường song song với nhau: Đúng.
b) Các xe chạy theo cùng một hướng: Sai.
Trong hình 4.5: Có 3 xe chạy theo hướng từ trên xuống dưới, 2 xe chạy thep hướng từ dưới lên trên
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau: Đúng.

a) Hàm số \(y = {x^2} - 3x + 2\)nghịch biến trên khoảng \(\left( { - \infty ;\frac{3}{2}} \right)\); đồng biến trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\)
b) Hàm số \(y = - 2{x^2} + 2x + 3\) đồng biến trên khoảng \(\left( { - \infty ;\frac{1}{2}} \right)\); nghịch biến trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\)
c) Hàm số \(y = {x^2} + 2x + 1\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\); đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\)
d) Hàm só \(y = - {x^2} + x - 1\) đồng biến trên khoảng \(\left( { - \infty ;\frac{1}{2}} \right)\); nghịch biến trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\)

a)
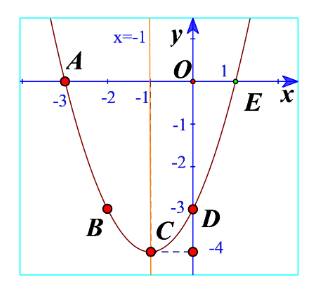
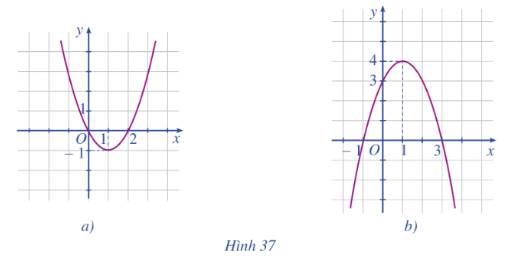
Hình 37a: Bề lõm hướng lên trên nên a>0
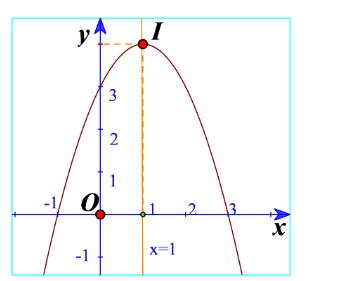
Hình 37b: Bề lõm xuống nên a<0
b)
Hình 37a: Đỉnh là (1;-1), trục đối xứng x=1
Hình 37b: Đỉnh là (1;4), trục đối xứng x=1
c)
Hình 37a: Hàm số đồng biến trên \(\left( {1; + \infty } \right)\)
Hình 37b: Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\)
d)
Hình 37a: Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\)
Hình 37b: Hàm số nghịch biến trên \(\left( {1; + \infty } \right)\)
e)
Hình 37a: Đồ thị nằm trên trục Ox khi \(x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
=> Khoảng giá trị x mà y > 0 là \(\left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
Hình 37b: Đồ thị nằm trên trục Ox khi \(x \in \left( { - 1;3} \right)\)
=> Khoảng giá trị x mà y > 0 là \(\left( { - 1;3} \right)\)
g)
Hình 37a: Đồ thị nằm dưới trục Ox khi \(x \in \left[ {0;2} \right]\)
=> Khoảng giá trị x mà y < 0 là \(\left[ {0;2} \right]\)
Hình 37b: Đồ thị nằm dưới trục Ox khi \(x \in \left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)
=> Khoảng giá trị x mà \(y \le 0\) là \(\left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)

a)
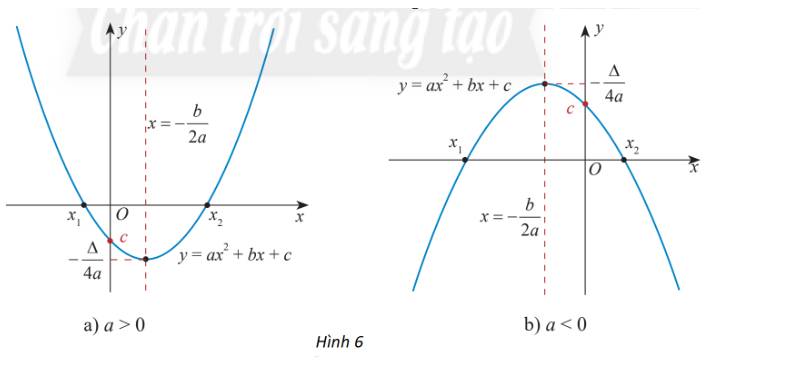
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \frac{b}{{2a}}; + \infty )\), khoảng nghịch biến là \(( - \infty ; - \frac{b}{{2a}})\)
b)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \infty ; - \frac{b}{{2a}})\), khoảng nghịch biến là \(( - \frac{b}{{2a}}; + \infty )\)