K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
29 tháng 5 2023
Bài này làm khá tắt chỗ 3 điểm cực trị, mình trình bày lại để bạn dễ hiểu nhé!
.......
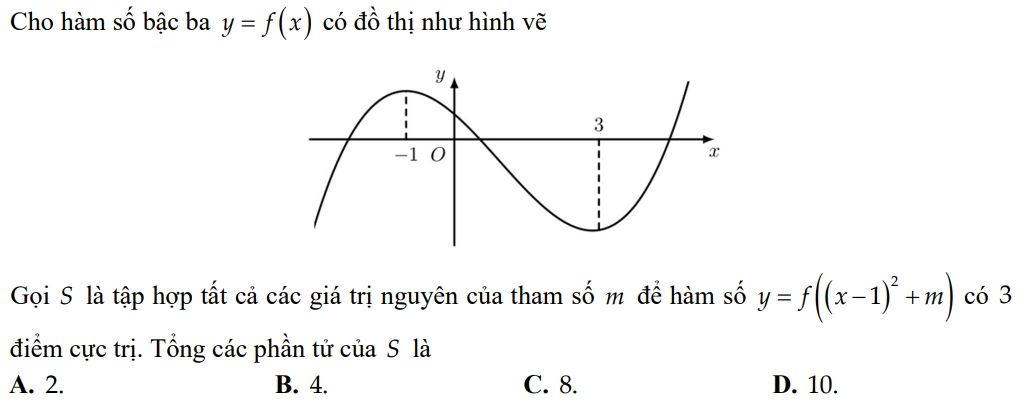
Để y' = 0\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f'\left(\left(x-1\right)^2+m\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2+m=-1\\\left(x-1\right)^2+m=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2=-1-m\left(1\right)\\\left(x-1\right)^2=3-m\left(2\right)\end{matrix}\right.\)
Để hàm số có 3 điểm cực trị thì y' = 0 có 3 nghiệm phân biệt.
Ta có 2 trường hợp.
+) \(TH_1:\) (1) có nghiệm kép x = 1 hoặc vô nghiệm và (2) có hai nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m\le0\\3-m>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge-1\\m< 3\end{matrix}\right.\) \(\Leftrightarrow-1\le m< 3\)
+) \(TH_2:\) (2) có nghiệm kép x = 1 và (2) có một nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m>0\\3-m\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m\ge3\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
\(\Rightarrow-1\le m< 3\Rightarrow S=\left\{-1;0;1;2\right\}\)
Do đó tổng các phần tử của S là \(-1+0+1+2=2\)
HP
14 tháng 9 2021
\(y=2-sin^2x-sin^2\left(m+x\right)-2cosm.cosx.cos\left(m+x\right)\)
\(=cos^2x+cos^2\left(m+x\right)-2cosm.cosx.cos\left(m+x\right)\)
\(=cos^2x+\left[cos\left(m+x\right)-2cosm.cosx\right].cos\left(m+x\right)\)
\(=cos^2x+\left[cosm.cosx-sinm.sinx-2cosm.cosx\right].cos\left(m+x\right)\)
\(=cos^2x-\left[sinm.sinx+cosm.cosx\right].cos\left(m+x\right)\)
\(=cos^2x-cos\left(m-x\right).cos\left(m+x\right)\)
\(=cos^2x-\dfrac{1}{2}\left(cos2m+cos2x\right)\)
\(=cos^2x-\dfrac{1}{2}cos2x-\dfrac{1}{2}cos2m\)
\(=cos^2x-\dfrac{1}{2}\left(2cos^2x-1\right)-\dfrac{1}{2}cos2m\)
\(=\dfrac{1}{2}-\dfrac{1}{2}cos2m\)
\(\Rightarrow\) Hàm số \(y=2-sin^2x-sin^2\left(m+x\right)-2cosm.cosx.cos\left(m+x\right)\) nhận giá trị không đổi trên R.
HT
10 tháng 4 2021
31/
\(3z^2-2z+27=0\)
\(\Delta'=\left(-1\right)^2-3.27=1-3.27=-80\)
\(\Delta'\) có 2 căn bậc 2 là \(\pm4i\sqrt{5}\)
\(\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1+4i\sqrt{5}}{3}\\z_2=\dfrac{1-4i\sqrt{5}}{3}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\left(\dfrac{1}{3}\right)^2+\left(\dfrac{4\sqrt{5}}{3}\right)^2}=3\)
\(\Rightarrow z_1\left|z_2\right|+z_2\left|z_1\right|=1+4i\sqrt{5}+1-4i\sqrt{5}=2\) => A
32/ \(\Delta'=4-29=-25\Rightarrow\left\{{}\begin{matrix}z_1=-2+5i\\z_2=-2-5i\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{2^2+5^2}=\sqrt{29}\)
\(\Rightarrow\left|z_1\right|^4+\left|z_2\right|^4=2.\sqrt{29^4}=1682\) => B
33/ \(\Delta=1-12=-11\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1+i\sqrt{11}}{6}\\z_2=\dfrac{1-i\sqrt{11}}{6}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\left(\dfrac{1}{6}\right)^2+\left(\dfrac{\sqrt{11}}{6}\right)^2}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\left|z_1\right|+\left|z_2\right|=\dfrac{2\sqrt{3}}{3}\) => D
34/ \(\Delta=1-4.3.2=-23\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1-i\sqrt{23}}{6}\\z_2=\dfrac{1+i\sqrt{23}}{6}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\dfrac{1}{36}+\dfrac{23}{36}}=\dfrac{\sqrt{6}}{3}\)
\(\Rightarrow T=2.\left(\dfrac{\sqrt{6}}{3}\right)^2=\dfrac{4}{3}\) => C
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 8 2021
a.
\(f'\left(x\right)=2cos2x-1=0\Rightarrow cos2x=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=-\dfrac{\pi}{6}\end{matrix}\right.\)
Ta có:
\(f\left(-\dfrac{\pi}{2}\right)=0+\dfrac{\pi}{2}=\dfrac{\pi}{2}\)
\(f\left(\dfrac{\pi}{2}\right)=0-\dfrac{\pi}{2}=-\dfrac{\pi}{2}\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}-\dfrac{\pi}{6}\)
\(f\left(-\dfrac{\pi}{6}\right)=-\dfrac{\sqrt{3}}{2}+\dfrac{\pi}{6}\)
So sánh các giá trị trên ta được:
\(f\left(x\right)_{max}=f\left(-\dfrac{\pi}{2}\right)=\dfrac{\pi}{2}\)
\(f\left(x\right)_{min}=f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 8 2021
b.
\(f'\left(x\right)=3-2\sqrt{3}sin2x=0\Rightarrow sin2x=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=\dfrac{\pi}{3}\end{matrix}\right.\)
Ta có: \(f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\pi}{2}+\dfrac{\sqrt{3}}{2}\)
\(f\left(\dfrac{\pi}{3}\right)=\pi-\dfrac{\sqrt{3}}{2}\)
\(f\left(\pi\right)=3\pi+\sqrt{3}\)
Từ đó: \(f_{min}=f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)
\(f_{max}=f\left(\pi\right)=3\pi+\sqrt{3}\)
HT
24 tháng 12 2016
\(y'=\left(2m+1\right)\cos x+3-m\)
Hàm số đã cho đồng biến trên R \(\Leftrightarrow y'\ge0,\forall x\in R\)
\(\Leftrightarrow\left(2m+1\right)\cos x\le m-3\) (1)
*TH: \(2m+1< 0\Leftrightarrow m< \frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\ge\frac{m-3}{2m+1}\) (không thoả với mọi x)
*TH: \(2m+1>0\Leftrightarrow m>\frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\le\frac{m-3}{2m+1}\) (2)
(2) đúng với mọi x khi và chỉ khi \(\left|\frac{m-3}{2m+1}\right|>1\Leftrightarrow\left[\begin{array}{nghiempt}m< -4\\m>\frac{2}{3}\end{array}\right.\)
kết hợp \(m>\frac{-1}{2}\) ta có m > 3/2 là giá trị cần tìm
DD
12 tháng 4 2016
2 mp (P) và (Q) // với nhau.→vecto pháp tuyến của mp này cũng là vecto pt của mặt phẳng kia, tìm vecto pt của một trong hai mặt phẳng bằng cách tìm đoạn vuông góc chung của 2 đường thẳng d1 và d2.
HP
Tìm tất cả các giá trị của m để pt \(8^{2x^2-2x-4}+m^2-m=0\) có nghiệm.
Mong m.n chỉ cho e cách giải.
4
4 tháng 3 2017
xét \(A=2x^2-2x-4=2\left[\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{4}\right]\ge-\dfrac{9}{2}\)
\(\Rightarrow8^{2x^2-2x-4}\ge\dfrac{1}{\sqrt{8^9}}\)
Để phương trình: \(8^{2x^2-2x-4}+m^2-m=0\) có nghiệm
Cần \(m-m^2\ge\dfrac{1}{\sqrt{8^9}}\Leftrightarrow m^2-m+\dfrac{1}{\sqrt{.8^9}}\le0\)
\(\Rightarrow\dfrac{1-\sqrt{1-\dfrac{4}{\sqrt{8^9}}}}{2}\le m\le\dfrac{1+\sqrt{1-\dfrac{4}{\sqrt{8^9}}}}{2}\)
=>không có đáp án nào tuyệt đối chính xác.
chọn phương B gần đúng nhất nhưng vẫn chưa đúng:
do \(\left\{{}\begin{matrix}\dfrac{1+\sqrt{1-\dfrac{4}{\sqrt{8^9}}}}{2}< 1\\\dfrac{1-\sqrt{1-\dfrac{4}{\sqrt{8^9}}}}{2}>0\end{matrix}\right.\).
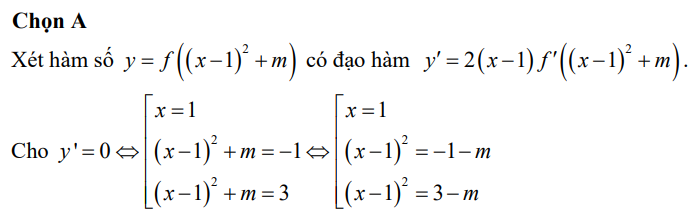
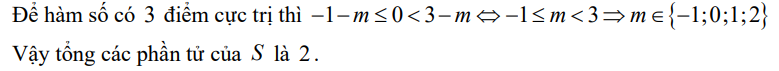
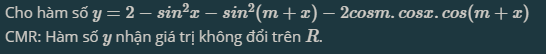
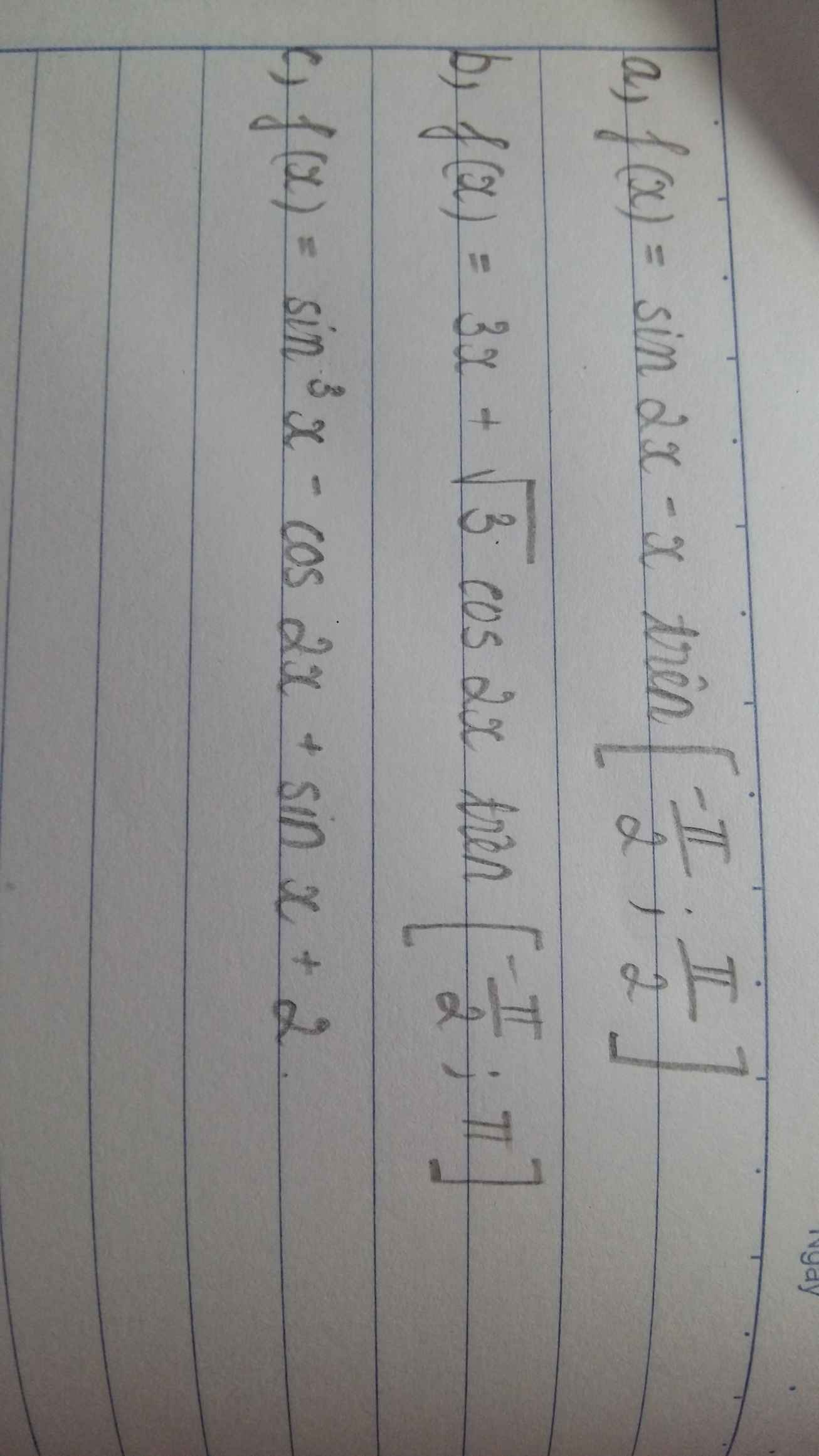
\(f'\left(x\right)=-2sinx.cosx-2sin\left(x+m\right).cos\left(x+m\right)+2cosm\left[sinx.cos\left(m+x\right)+cosx.sin\left(m+x\right)\right]\)
\(=-sin2x-sin\left(2x+2m\right)+2cosm.sin\left(2x+m\right)\)
\(=-2sin\left(2x+m\right).cosm+2cosm.sin\left(2x+m\right)\)
\(=0\)
b. Do \(f'\left(x\right)=0\) với mọi x \(\Rightarrow f\left(x\right)\) là hàm hằng \(\Rightarrow f\left(x\right)\) nhận giá trị ko đổi trên R