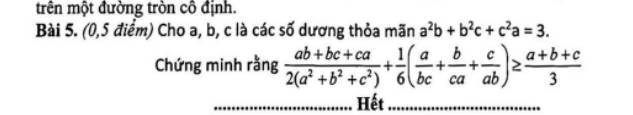K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9L
2
9 tháng 11 2021
\(ĐK:x\ge2013\\ PT\Leftrightarrow\sqrt{x-2013}+2\sqrt{x-2013}=3\\ \Leftrightarrow3\sqrt{x-2013}=3\\ \Leftrightarrow\sqrt{x-2013}=1\Leftrightarrow x-2013=1\\ \Leftrightarrow x=2014\left(tm\right)\)
NI
9 tháng 11 2021
\(\sqrt{x-2013}+\sqrt{4x-8052}=3\)
\(\Leftrightarrow\sqrt{x-2013}+\sqrt{4\left(x-2013\right)}=3\)
\(\Leftrightarrow\sqrt{x-2013}+2\sqrt{x-2013}=3\)
\(\Leftrightarrow3\sqrt{x-2013}=3\)
\(\Leftrightarrow\sqrt{x-2013}=1\)
\(\Leftrightarrow x-2013=1\)
\(\Leftrightarrow x=2014\)
7 tháng 10 2021
Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)
19 tháng 8 2021
Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
19 tháng 8 2021
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
Ta có:
\(\dfrac{ab+bc+ca}{2\left(a^2+b^2+c^2\right)}+\dfrac{1}{6}\left(\dfrac{a^2+b^2+c^2}{abc}\right)\ge2\sqrt{\dfrac{1}{12}\left(\dfrac{ab+ca+ca}{abc}\right)}=\sqrt{3\left(\dfrac{ab+bc+ca}{abc}\right)}\)
Nên ta chỉ cần cm:
\(\sqrt{\dfrac{1}{3}\left(\dfrac{ab+bc+ca}{abc}\right)}\ge\dfrac{a+b+c}{3}\Leftrightarrow3\left(\dfrac{ab+bc+ca}{abc}\right)\ge\left(a+b+c\right)^2\)
Thật vậy, ta có:
\(\dfrac{3\left(ab+bc+ca\right)}{abc}=\dfrac{\left(a^2b+b^2c+c^2a\right)\left(ab+bc+ca\right)}{abc}\)
\(=\left(\dfrac{a}{c}+\dfrac{b}{a}+\dfrac{c}{b}\right)\left(ac+ab+bc\right)\ge\left(a+b+c\right)^2\) (Bunhiacopxki)
Dấu "=" xảy ra khi \(a=b=c=1\)
TN
1
27 tháng 9 2021
Câu 5:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: Xét tứ giác AEDF có
\(\widehat{EAF}=\widehat{AFD}=\widehat{AED}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác của \(\widehat{FAE}\)
nên AEDF là hình vuông
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2
TG
30 tháng 6 2021
Bài 2:
\(\sqrt{2x-1}=5\)
=> 2x - 1 = 25
=> 2x = 26
=> x = 13
b) \(\sqrt[3]{3x+2}=-3\)
=> 3x + 2 = -27
=> 3x = -29
=> x = -29/3
P/s: Mỗi lần chỉ đc hỏi 1 bài thôi em nehs!
30 tháng 6 2021
1. ĐK:
a, \(x\ge\dfrac{5}{2}\)
b, \(\left\{{}\begin{matrix}x\ge0\\x\ne\dfrac{9}{4}\end{matrix}\right.\)
2.
a,ĐK: \(x\ge\dfrac{1}{2}\)
PT\(\Leftrightarrow2x-1=25\Rightarrow x=13\left(tm\right)\)
b,ĐK: \(\forall x\in R\)
PT\(\Leftrightarrow3x+2=-27=>x=-\dfrac{29}{3}\) (tm)
3.
a,\(\sqrt{5}.\sqrt{1,2}.\sqrt{24}=\sqrt{120}.\sqrt{1,2}=12\)
b,\(\dfrac{\sqrt{4444}}{\sqrt{1111}}=\dfrac{\sqrt{4}.\sqrt{1111}}{\sqrt{1111}}=2\)
c,\(\sqrt{\dfrac{3}{5}}+\sqrt{\dfrac{5}{3}}-\dfrac{1}{2}\sqrt{60}=\dfrac{8}{\sqrt{15}}-\sqrt{15}=-\dfrac{7}{\sqrt{15}}\)
d,\(\sqrt{5+2\sqrt{6}}+\sqrt{5-2\sqrt{6}}=\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}=2\sqrt{3}\)
AH
Akai Haruma
Giáo viên
31 tháng 7 2021
Bài 1:
Nếu chị nhớ không nhầm thì phải là \(\left[\begin{matrix} \frac{1}{2}\leq x< 2\\ 0< x<\frac{1}{2}\end{matrix}\right.\)
Tức là $x$ nhận các khoảng giá trị sau:
\(0< x< \frac{1}{2}\); \(x=\frac{1}{2}\); \(\frac{1}{2}< x< 2\)
Vậy có nghĩa $0< x< 2$ (rất dễ hiểu mà????)
AH
Akai Haruma
Giáo viên
31 tháng 7 2021
Bài 2:
Ngoặc nhọn dùng khi muốn biểu thị hai/ nhiều phương trình/ bất phương trình đồng thời xảy ra cùng một lúc
Ngoặc vuông dùng khi muốn biểu thị cái này hoặc cái kia xảy ra.
Bài trên phải dùng ngoặc vuông là sao em? Ngoặc nhọn thường xuất hiện trong bài toán giải hệ phương trình, bất phương trình. Còn ngoặc vuông thì thường dùng kết luận nghiệm của pt/ bpt.
Kết hợp điều kiện thì dùng ngoặc nhọn. Ví dụ $\sqrt{x+1}+\sqrt{2-x}$ thì việc $x+1\geq 0$ và $2-x\geq 0$ phải đồng thời xảy ra cùng lúc.