
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mình làm vài câu cho bạn tham khảo,các câu còn lại thì bạn làm tương tự thôi
23.\(\sqrt{14-2\sqrt{33}}=\sqrt{\left(\sqrt{11}\right)^2-2.\sqrt{11}.\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{\left(\sqrt{11}-\sqrt{3}\right)^2}=\left|\sqrt{11}-\sqrt{3}\right|=\sqrt{11}-\sqrt{3}\)
28. \(\sqrt{25-4\sqrt{6}}=\sqrt{\left(2\sqrt{6}\right)^2-2.2\sqrt{6}.1+1^2}=\sqrt{\left(2\sqrt{6}-1\right)^2}\)
\(=\left|2\sqrt{6}-1\right|=2\sqrt{6}-1\)
29.\(\sqrt{14-8\sqrt{3}}=\sqrt{14-2\sqrt{48}}=\sqrt{\left(\sqrt{8}\right)^2-2\sqrt{6}.\sqrt{8}+\left(\sqrt{6}\right)^2}\)
\(=\sqrt{\left(\sqrt{8}-\sqrt{6}\right)^2}=\left|\sqrt{8}-\sqrt{6}\right|=\sqrt{8}-\sqrt{6}\)



Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....

1: Ta có: \(\sqrt{3x-5}=2\)
\(\Leftrightarrow3x-5=4\)
hay x=3
2: Ta có: \(\sqrt{25\left(x-1\right)}=20\)
\(\Leftrightarrow x-1=16\)
hay x=17

2.c
\(x+\sqrt{4x^2-4x+1}=5\)
\(\Leftrightarrow x+\sqrt{\left(2x-1\right)^2}=5\)
\(\Leftrightarrow x+\left|2x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2x-1=5;x\ge\dfrac{1}{2}\\x+1-2x=5;x< \dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}3x=6\\-x=4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=-4\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{2;-4\right\}\)

a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)







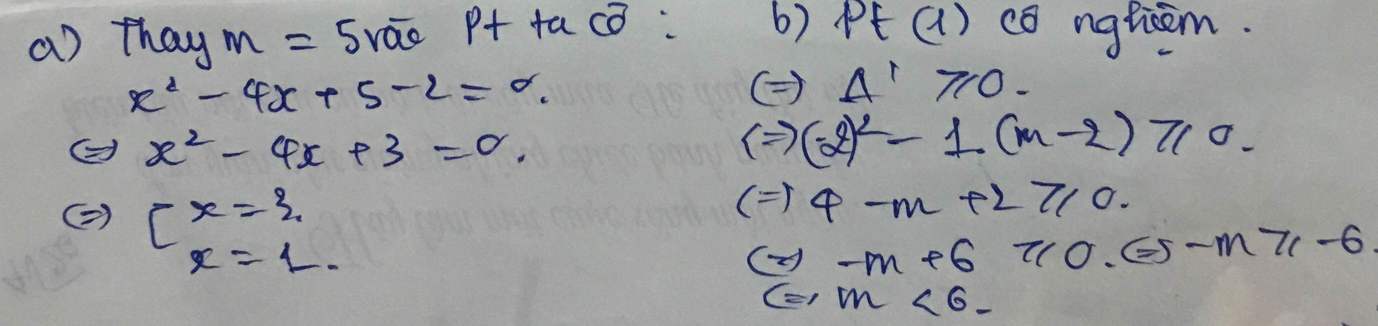
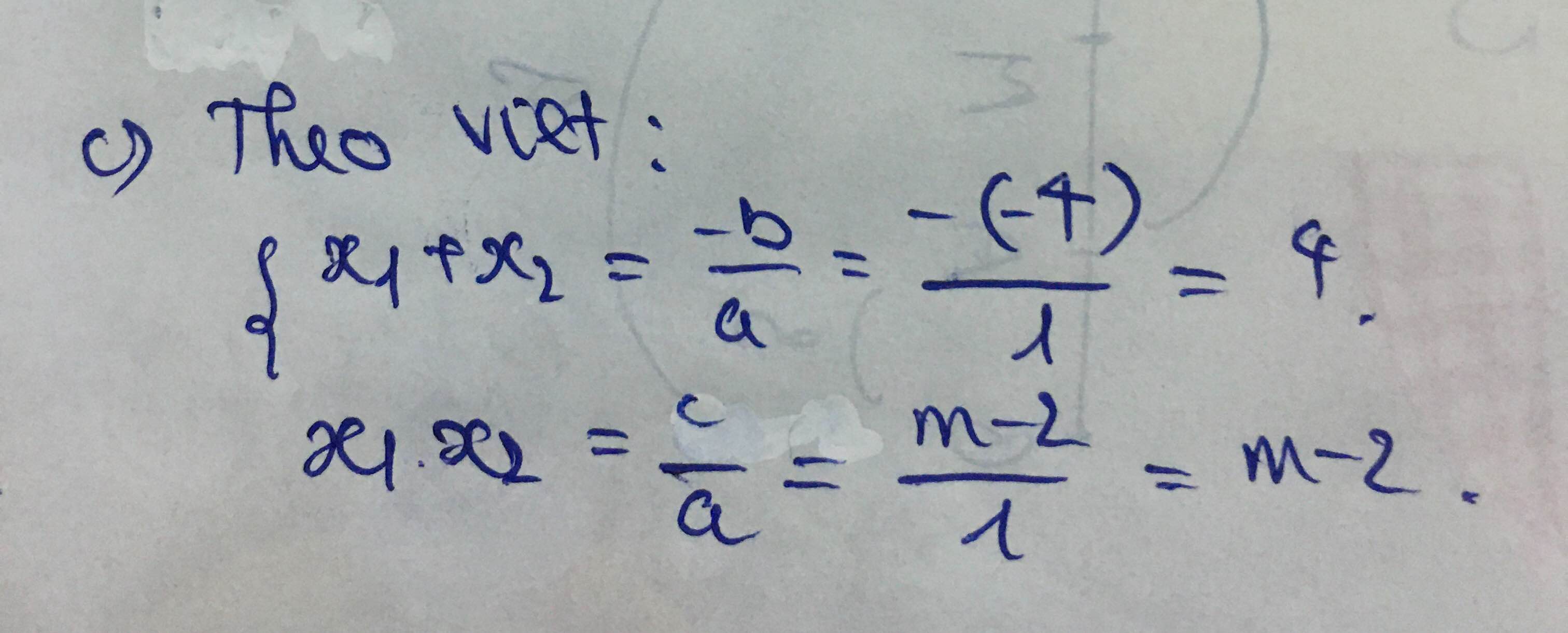
 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 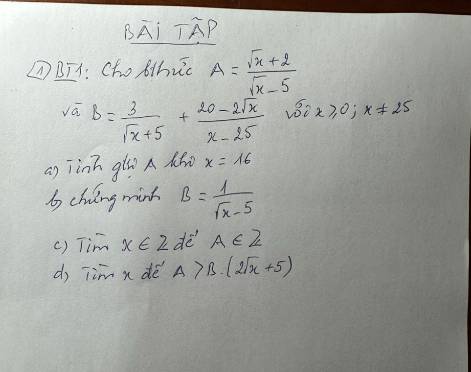
 giúp mình câu 4 với câu 2 phần 2 với
giúp mình câu 4 với câu 2 phần 2 với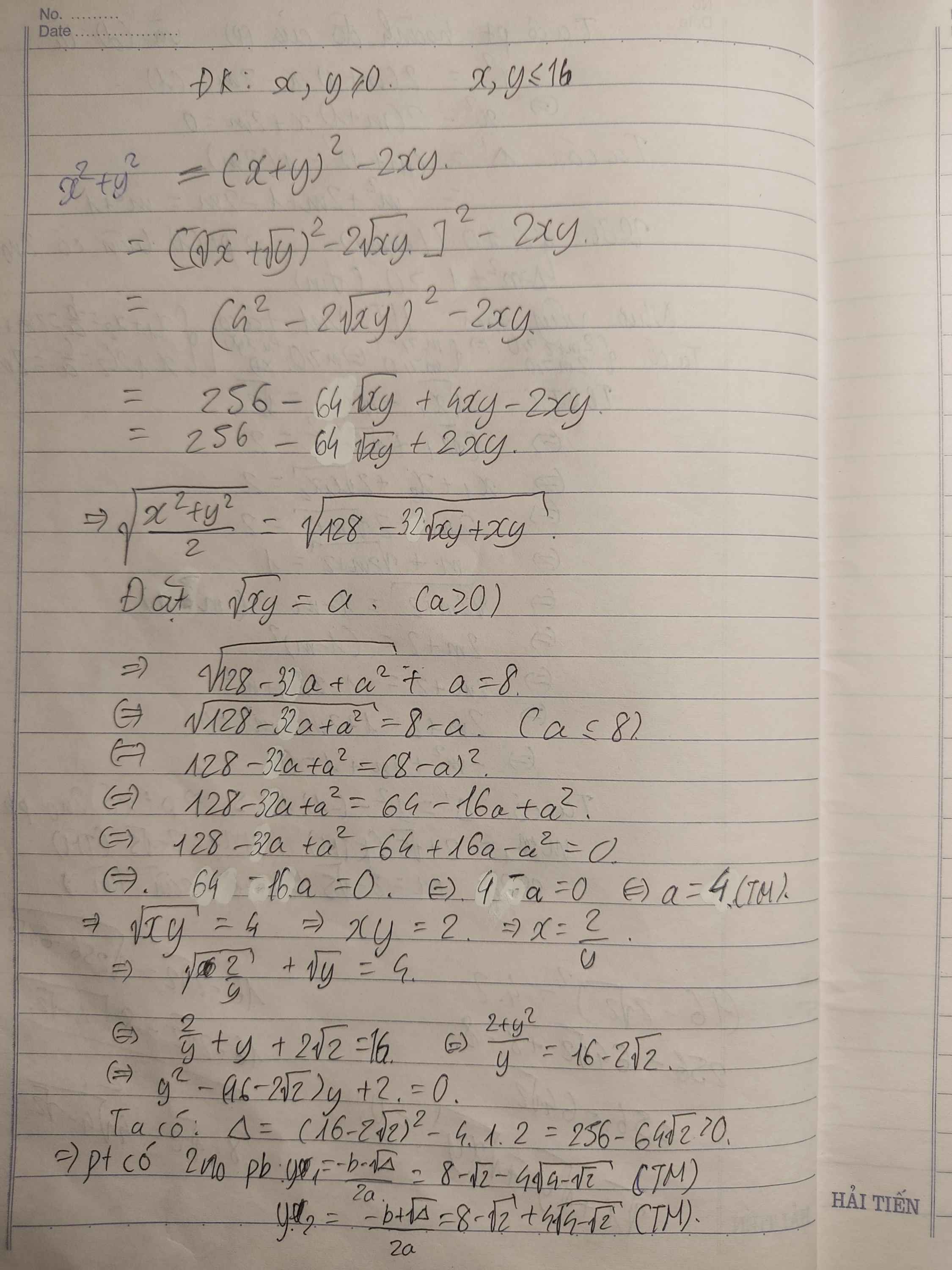
\(a+b+c-21=2\left(\sqrt{a-7}+\sqrt{b-8}+\sqrt{c-9}\right)\)
\(\Leftrightarrow a-7-2\sqrt{a-7}+1+b-8-2\sqrt{b-8}+1+c-9-2\sqrt{c-9}+1=0\)
\(\Leftrightarrow\left(\sqrt{a-7}-1\right)^2+\left(\sqrt{b-8}-1\right)^2+\left(\sqrt{c-9}-1\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}\sqrt{a-7}-1=0\\\sqrt{b-8}-1=0\\\sqrt{c-9}-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=8\\b=9\\c=10\end{cases}}\)
\(S=a+2b-c=8+2.9-10=16\)
Chọn A.
\(a+b+c-21-2\left(\sqrt{a-7}+\sqrt{b-8}+\sqrt{c-9}\right)=0\)
\(a-7-2\sqrt{a-7}+1+b-8-2\sqrt{b-8}+1+c-9-2\sqrt{c-9}+1=0\)
\(\left(\sqrt{a-7}-1\right)^2+\left(\sqrt{b-8}-1\right)^2+\left(\sqrt{c-9}-1\right)^2=0\)
\(\hept{\begin{cases}\sqrt{a-7}-1=0\\\sqrt{b-8}-1=0\\\sqrt{c-9}-1==0\end{cases}}\)
\(\hept{\begin{cases}a=8\\b=9\\c=10\end{cases}}\)
\(8+2.9-10=16\)
chon A
\(\)