K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
3
22 tháng 11 2023
Bài 1:
3: ĐKXĐ: x>=1
\(x-\sqrt{x+3+4\sqrt{x-1}}=1\)
=>\(x-\sqrt{x-1+2\cdot\sqrt{x-1}\cdot2+4}=1\)
=>\(x-\sqrt{\left(\sqrt{x-1}+2\right)^2}=1\)
=>\(x-\left|\sqrt{x-1}+2\right|=1\)
=>\(x-\left(\sqrt{x-1}+2\right)=1\)
=>\(x-\sqrt{x-1}-2-1=0\)
=>\(x-1-\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}+\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}-2\right)\left(\sqrt{x-1}+1\right)=0\)
=>\(\sqrt{x-1}-2=0\)
=>\(\sqrt{x-1}=2\)
=>x-1=4
=>x=5(nhận)
KT
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
1
14 tháng 10 2021
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
18 tháng 7 2023
3, ta có:
\(B=\dfrac{\sqrt{x}-3+2\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x-3}\right)}\cdot\dfrac{2\left(\sqrt{x}+3\right)}{\sqrt{x}-1}\\ =\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{2\left(\sqrt{x}+3\right)}{\sqrt{x}-1}\\ =\dfrac{6}{\sqrt{x}-3}\)
để B=3 thì ta có:
\(\dfrac{6}{\sqrt{x}-3}=3\\ \Leftrightarrow\dfrac{6}{\sqrt{x}-3}=\dfrac{3\sqrt{x}-9}{\sqrt{x}-3}\\ \Leftrightarrow6=3\sqrt{x}-9\\ \Leftrightarrow3\sqrt{x}=15\\ \Leftrightarrow\sqrt{x}=5\\ \Leftrightarrow x=25\)
vậy để B=3 thì x=25
H
2 tháng 6 2023
\(\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{x}-\sqrt{y}\right)^2=0\\\sqrt{x}+\sqrt{y}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-\sqrt{y}=0\\\sqrt{x}+\sqrt{y}=1\end{matrix}\right.\)
\(\Rightarrow2\sqrt{x}=1\Rightarrow x=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
\(\Rightarrow y=\dfrac{1}{4}\)
Vậy hệ phương trình có tập nghiệm \(S=\left(\dfrac{1}{4};\dfrac{1}{4}\right)\)
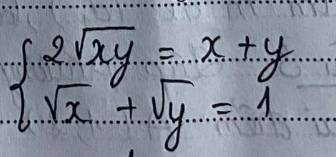
3: Xét ΔOHF vuông tại H và ΔOEM vuông tại E có
\(\widehat{HOF}\) chung
Do đó: ΔOHF đồng dạng với ΔOEM
=>\(\dfrac{OH}{OE}=\dfrac{OF}{OM}\)
=>\(OH\cdot OM=OE\cdot OF\)(1)
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\left(2\right)\)
Từ (1) và (2) suy ra \(OE\cdot OF=OA^2\)
=>\(OE\cdot OF=OC^2\)
=>\(\dfrac{OE}{OC}=\dfrac{OC}{OF}\)
Xét ΔOEC và ΔOCF có
\(\dfrac{OE}{OC}=\dfrac{OC}{OF}\)
\(\widehat{COE}\) chung
Do đó: ΔOEC\(\sim\)ΔOCF
=>\(\widehat{OEC}=\widehat{OCF}=90^0\)
=>CF là tiếp tuyến của (O)