K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 1 2022
Câu 24:
Để phương trình có hai nghiệm trái dấu thì \(\left(m^2+2020\right)\left(m-2021\right)< 0\)
=>m<2021
mà m nguyên dương
nên \(m\in\left\{1;...;2020\right\}\)
=>có 2020 số
C1
1
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2022
Pt bậc 2 có 2 nghiệm trái dấu khi \(ac< 0\)
\(\Leftrightarrow\left(m^2-4\right)m< 0\)
\(\Leftrightarrow m\in\left(-\infty;-2\right)\cup\left(0;2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2021
\(\overrightarrow{MN}=\left(2;2\right)\Rightarrow MN=\sqrt{2^2+2^2}=2\sqrt{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\sqrt{2}\)
Gọi I là tâm đường tròn đường kính MN \(\Rightarrow\) I là trung điểm MN
\(\Rightarrow I\left(0;2\right)\)
Phương trình (C): \(x^2+\left(y-2\right)^2=2\)
b.
Tiếp tuyến d' song song d nên nhận \(\left(3;-5\right)\) là 1 vtpt
Phương trình d' có dạng: \(3x-5y+c=0\)
d' là tiếp tuyến của (C) nên: \(d\left(I;d'\right)=R\)
\(\Leftrightarrow\dfrac{\left|3.0-5.2+c\right|}{\sqrt{3^2+\left(-5\right)^2}}=\sqrt{2}\Leftrightarrow\left|c-10\right|=2\sqrt{17}\)
\(\Rightarrow\left[{}\begin{matrix}c=10+2\sqrt{17}\\c=10-2\sqrt{17}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}3x-5y+10+2\sqrt{17}=0\\3x-5y+10-2\sqrt{17}=0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 12 2021
\(5\overrightarrow{v}=3\overrightarrow{b}-2\overrightarrow{a}\Rightarrow\overrightarrow{v}=\dfrac{3}{5}\overrightarrow{b}-\dfrac{2}{5}\overrightarrow{a}=\dfrac{3}{5}\left(-1;2\right)-\dfrac{2}{5}\left(3;-4\right)=\left(-\dfrac{9}{5};\dfrac{14}{5}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2021
\(sin^2x=\left(sinx\right)^2\ne sin\left(x^2\right)\)
1 cái là bình phương của cả hàm sin, 1 cái chỉ là bình phương của góc
Cách giải bài này: suy nghĩ đầu tiên: hạ bậc.
Đầu tiên chắc chắn là phải biến đổi \(-sin^2a-sin^2b\) (phần \(sin^2\left(a+b\right)\) nếu áp dụng \(sin^2\left(a+b\right)=\left(sina.cosb+cosa.sinb\right)^2\) thì khai triển ra sẽ rất thảm họa nên cứ để đó từ từ tính sau)
\(-sin^2a-sin^2b=-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2a\right)-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2b\right)\) (công thức hạ bậc)
\(=-1+\dfrac{1}{2}\left(cos2a+cos2b\right)=-1+cos\left(a+b\right)cos\left(a-b\right)\) (công thức biến tổng thành tích)
Thấy xuất hiện góc \(\left(a+b\right)\) giống góc của \(sin^2\left(a+b\right)\) rồi, nhưng của hàm cos, vậy thì đơn giản hãy biến \(sin^2\left(a+b\right)\) thành hàm cos bằng công thức cơ bản: \(sin^2\left(a+b\right)=1-cos^2\left(a+b\right)\)
Do đó, chắc chắn bài toán sẽ được giải quyết như sau:
\(A=1-cos^2\left(a+b\right)-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2a\right)-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2b\right)\)
\(A=-cos^2\left(a+b\right)+\dfrac{1}{2}\left(cos2a+cos2b\right)\)
\(A=-cos^2\left(a+b\right)+cos\left(a+b\right)cos\left(a-b\right)\)
\(=cos\left(a+b\right)\left[cos\left(a-b\right)-cos\left(a+b\right)\right]\)
\(=2sina.sinb.cos\left(a+b\right)\)
(Sử dụng biến tổng thành tích: \(cosx-cosy=-2sin\dfrac{x+y}{2}sin\dfrac{x-y}{2}\)
Thì: \(cos\left(a-b\right)-cos\left(a+b\right)=-2sin\dfrac{a-b+a+b}{2}sin\dfrac{a-b-a-b}{2}=-2sina.sin\left(-b\right)=2sina.sinb\)
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
Lời giải:
a. TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(x)=|x|=|-x|=f(-x)$
$\Rightarrow $ hàm chẵn
b. TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=9; -f(1)=-9; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$ nên hàm không chẵn không lẻ.
c.
TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(-x)=(-x)^3+(-x)=-(x^3+x)=-f(x)$ nên hàm lẻ
d.
TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=3; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$
Do đó hàm không chẵn không lẻ.
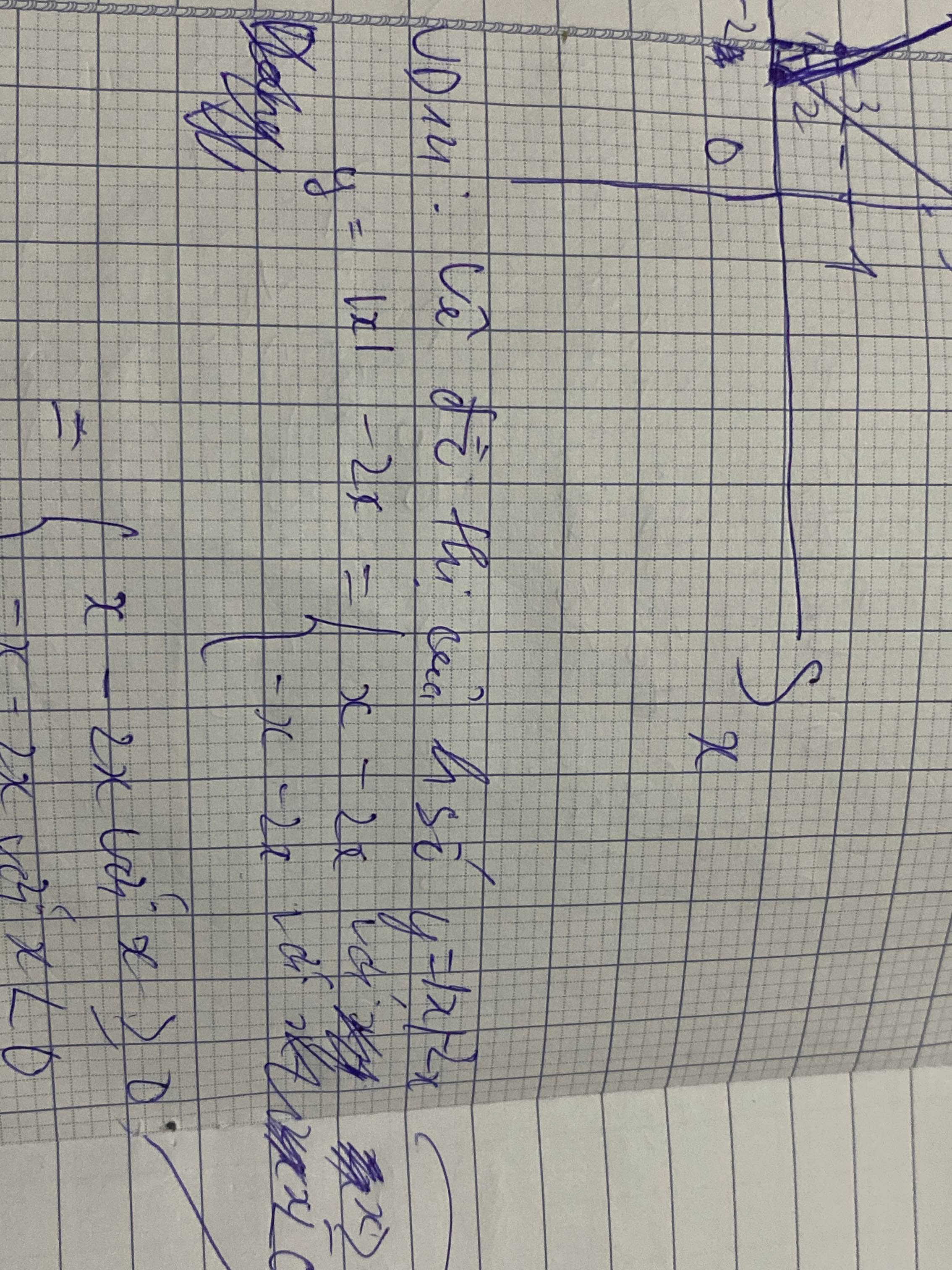
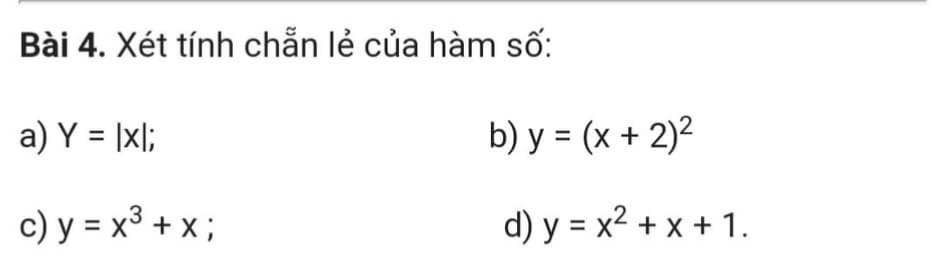
Lý thuyết: \(\left(\overrightarrow{a};\overrightarrow{b}\right)=180^0-\left(-\overrightarrow{a};\overrightarrow{b}\right)\)
Ta có: \(\left(\overrightarrow{CA};\overrightarrow{CB}\right)=\widehat{C}=40^0\Rightarrow\left(\overrightarrow{AC};\overrightarrow{CB}\right)=180^0-40^0=140^0\)