Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(W_đ=W_t\Rightarrow x =\pm\dfrac{A}{\sqrt 2}\)
Như vậy, để \(W_t < W_đ\) thì: \(|x| <\dfrac{A}{\sqrt 2}\)
Biểu điễn bằng véc tơ quay, ta tìm đc khoảng thời gian tương ứng này bằng T/4 = 2/4 = 0,5s
Chọn A.

Đáp án A
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
Theo đề bài ta có
![]()
![]()
Biểu diễn trên đường tròn lượng giác ta có :
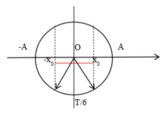
Từ đường tròn lượng giác ta thấy phần gạch đỏ là phần thỏa mãn yên cầu của đề bài => x0 = A/2 = 2,5 cm
Do đó ta có :
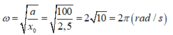
=> Tần số f = ω / 2 π => Chọn A

Để tìm tần số dao động của con lắc, ta có công thức:
f = 1/T
Trong đó: f là tần số dao động (Hz) T là chu kì dao động (s)
Theo đề bài, khoảng thời gian để vật nhỏ của con lắc có độ lớn gia tốc không vượt quá 100 cm/s là T/3. Độ lớn gia tốc của con lắc được tính bằng công thức:
a = -ω²x
Trong đó: a là gia tốc (cm/s²) ω là góc tốc độ góc của con lắc (rad/s) x là biên độ dao động (cm)
Ta có thể tính được ω bằng công thức:
ω = 2πf
Thay vào công thức gia tốc, ta có:
a = -(2πf)²x = -4π²f²x
Đề bài cho biết gia tốc không vượt quá 100 cm/s, nên ta có:
100 ≥ 4π²f²x
Với x = 5 cm, ta có:
100 ≥ 4π²f²(5)
Simplifying the equation:
5 ≥ π²f²
Từ đó ta có:
f² ≤ 5/π²
f ≤ √(5/π²)
f ≤ √(5/π²) ≈ 0.798 Hz
Vậy tần số dao động của con lắc là khoảng 0.798 Hz.





|v|\(\leq \)10\(π\)(cm/s)
T=1s =>\(\omega \)=\(\frac{2π }{T}\)=\(2π\)(rad/s)
vmax=\(\omega .A\)=\(2π\).10=20\(π\)(cm/s)
\(\alpha \)=\(\frac{π }{3}\)
t=\(\frac{2\alpha }{\omega }\)=\(\frac{2. π/3}{2π}\)=1/3s
=>đáp án D.1/3s
cảm ơn nha