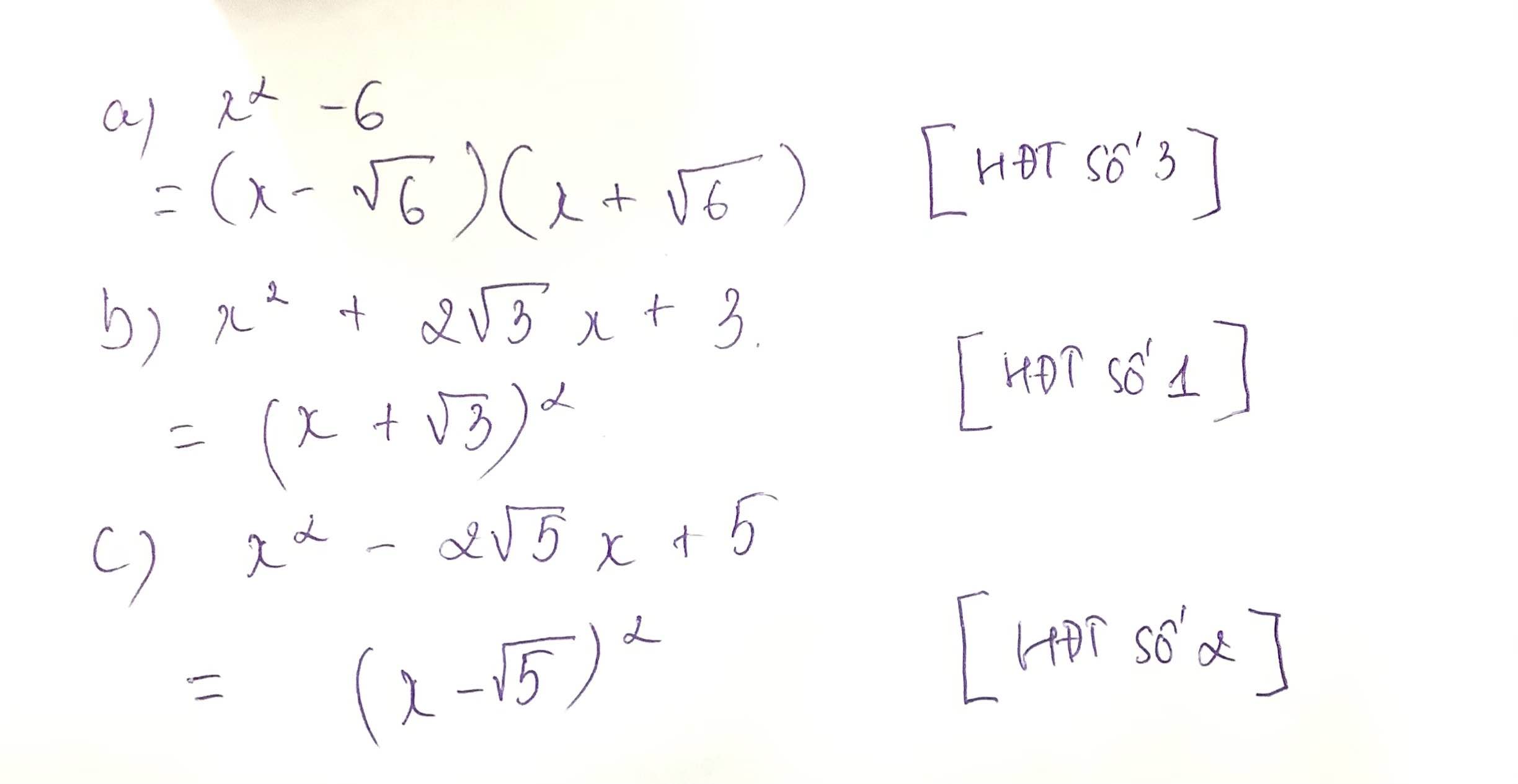K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 8 2016
Ta có : \(\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}=\frac{\left(\sqrt{5}-\sqrt{3}\right)^2}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}=\frac{8-2\sqrt{15}}{2}=4-\sqrt{15}\)
Thay \(x=4-\sqrt{15}\) vào pt được :
\(\left(4-\sqrt{15}\right)^2.a+\left(4-\sqrt{15}\right)b+1=0\Leftrightarrow\left(31-8\sqrt{15}\right)a+\left(4-\sqrt{15}\right)b+1=0\)
\(\Leftrightarrow\sqrt{15}\left(-8a-b\right)+\left(31a+4b+1\right)=0\)
Vì a,b là số hữu tỉ nên ta có : \(\begin{cases}8a+b=0\\31a+4b=-1\end{cases}\) \(\Leftrightarrow\begin{cases}a=1\\b=-8\end{cases}\)
15 tháng 8 2016
Ta có:\(x=\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}=\frac{\left(\sqrt{5}-\sqrt{3}\right)^2}{5-3}=\frac{8-2\sqrt{15}}{2}=4-\sqrt{15}\)
Thay vào ta có:
\(a\cdot\left(4-\sqrt{15}\right)^2+b\cdot\left(4-\sqrt{15}\right)+1=0\)
\(\Leftrightarrow a\cdot\left(31-8\cdot\sqrt{15}\right)+4b-b\cdot\sqrt{15}+1=0\)
\(\Leftrightarrow\left(31a+4b+1\right)-\left(8a+b\right)\cdot\sqrt{15}=0\)
Do a,b hữu tỉ \(\Rightarrow\begin{cases}31a+4b+1=0\\8a+b=0\end{cases}\)\(\Leftrightarrow\begin{cases}31a-32a+1=0\\b=-8a\left(1\right)\end{cases}\)
31a-3a+1=0 <=>a=1.Từ (1) =>b=-8
Vậy a= 1 và b= -8
FZ
1
M
0
LV
3
HN
13 tháng 8 2021
a, \(x^2-6=x^2-\sqrt{6^2}=\left(x-\sqrt{6}\right)\left(x+\sqrt{6}\right)\)
b, \(x^2+2\sqrt{3}x+3=x^2+2\sqrt{3}x+\sqrt{3}=\left(x+\sqrt{3}\right)^2=\left(x+\sqrt{3}\right)\left(x+\sqrt{3}\right)\)
c, \(x^2-2\sqrt{5}x+5=x^2-2\sqrt{5}x+\sqrt{5}=\left(x-\sqrt{5}\right)^2=\left(x-\sqrt{5}\right)\left(x-\sqrt{5}\right)\)
10 tháng 8 2023
\(\Leftrightarrow\sqrt{x+3}-2-2\sqrt{x}+2=\sqrt{2x+2}-2+2-\sqrt{3x+1}\)
=>\(\dfrac{x+3-4}{\sqrt{x+3}+2}-2\left(\sqrt{x}-1\right)=\dfrac{2x+2-4}{\sqrt{2x+2}+2}+\dfrac{4-3x-1}{2+\sqrt{3x+1}}\)
=>\(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x+3}+2}-2\left(\sqrt{x}-1\right)=\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{2x+2}+2}-\dfrac{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{2+\sqrt{3x+1}}\)
=>\(\left(\sqrt{x}-1\right)\left(\dfrac{\sqrt{x}+1}{\sqrt{x+3}+2}-2-\dfrac{2\sqrt{x}+2}{\sqrt{2x+2}+2}+\dfrac{3\sqrt{x}+3}{2+\sqrt{3x+1}}\right)=0\)
=>căn x-1=0
=>x=1
M
0
NB
1
3 tháng 11 2017
a, \(x.\sqrt{\frac{2}{5}}\) = \(\sqrt{x^2}.\sqrt{\frac{2}{5}}\) = \(\sqrt{\frac{x^2.2}{5}}\)
b, \(\left(x-5\right).\sqrt{\frac{x}{25-x^2}}\)= \(\sqrt{\left(x-5\right)^2}\). \(\sqrt{\frac{x}{\left(5-x\right)\left(5+x\right)}}\) = \(\sqrt{\frac{\left(x-5\right)^2.x}{\left(x-5\right)\left(x+5\right)}}\)= \(\sqrt{\frac{x.\left(x-5\right)}{x+5}}\)
c,\(x.\sqrt{\frac{7}{x^2}}\) = \(\sqrt{x^2}\). \(\sqrt{\frac{7}{x^2}}\) = \(\sqrt{\frac{x^2.7}{x^2}}\) = \(\sqrt{7}\)