K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 12 2023
a: x-1 là bội của x+2
=>\(x-1⋮x+2\)
=>\(x+2-3⋮x+2\)
=>\(-3⋮x+2\)
=>\(x+2\inƯ\left(-3\right)\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)
b: 3x+1 là ước của x+2
=>\(x+2⋮3x+1\)
=>\(3x+6⋮3x+1\)
=>\(3x+1+5⋮3x+1\)
=>\(5⋮3x+1\)
=>\(3x+1\in\left\{1;-1;5;-5\right\}\)
=>\(3x\in\left\{0;-2;4;-6\right\}\)
=>\(x\in\left\{0;-\dfrac{2}{3};\dfrac{4}{3};-2\right\}\)
mà x nguyên
nên \(x\in\left\{0;-2\right\}\)
c: x+3 là ước của 2x+1
=>\(2x+1⋮x+3\)
=>\(2x+6-7⋮x+3\)
=>\(-7⋮x+3\)
=>\(x+3\in\left\{1;-1;7;-7\right\}\)
=>\(x\in\left\{-2;-4;4;-10\right\}\)
d: 3x+2 là bội của 2x-1
=>\(3x+2⋮2x-1\)
=>\(6x+4⋮2x-1\)
=>\(6x-3+7⋮2x-1\)
=>\(7⋮2x-1\)
=>\(2x-1\in\left\{1;-1;7;-7\right\}\)
=>\(2x\in\left\{2;0;8;-6\right\}\)
=>\(x\in\left\{1;0;4;-3\right\}\)
NM
3
8 tháng 11 2018
\(9^{2n}-6=81^n-6\)
\(\text{Vì }\orbr{\begin{cases}81^n⋮9\\6⋮9̸\end{cases}}\Rightarrow81^n-6⋮9̸\)
\(\Rightarrow9^{2n}-6⋮9̸\)
\(⋮̸\)là không chia hết
LT
2
9 tháng 5 2019
\(\frac{4}{7}x-\frac{2}{3}=\frac{1}{5}\)
\(\Leftrightarrow\frac{4}{7}x=\frac{1}{5}+\frac{2}{3}\)
\(\Leftrightarrow\frac{4}{7}x=\frac{3}{15}+\frac{10}{15}\)
\(\Leftrightarrow\frac{4}{7}x=\frac{13}{15}\)
\(\Leftrightarrow x=\frac{13}{15}:\frac{4}{7}=\frac{13}{15}\cdot\frac{7}{4}=\frac{91}{60}\)
DT
2
4 tháng 9 2016
\(B=\left(\frac{1}{4}-1\right)\cdot\left(\frac{1}{9}-1\right).....\left(\frac{1}{81}-1\right)\cdot\left(\frac{1}{100}-1\right)\)
\(B=\frac{-3}{4}\cdot\frac{-8}{9}....\frac{-80}{81}\cdot\frac{-99}{100}\)
\(B=-\left(\frac{3}{4}\cdot\frac{8}{9}\cdot\cdot\cdot\cdot\frac{99}{100}\right)\)
\(B=-\left(\frac{3\cdot8\cdot15\cdot24\cdot....\cdot63\cdot80\cdot99}{2^2\cdot3^2\cdot4^2\cdot\cdot\cdot\cdot\cdot9^2\cdot10^2}\right)\)
\(B=-\left(\frac{1\cdot3\cdot2\cdot4\cdot3\cdot5\cdot\cdot\cdot\cdot8\cdot10\cdot9\cdot11}{2^2\cdot3^2\cdot4^2\cdot\cdot\cdot\cdot9^2\cdot10^2}\right)\)
\(B=-\frac{11}{2\cdot10}\)
\(B=\frac{-11}{20}\)
4 tháng 9 2016
\(B=\left(\frac{1}{4}-1\right).\left(\frac{1}{9}-1\right)...\left(\frac{1}{100}-1\right)\)
\(B=\frac{-3}{2^2}.\frac{-8}{3^2}...\frac{-99}{10^2}\)
\(B=-\left(\frac{3}{2^2}.\frac{8}{3^2}...\frac{99}{10^2}\right)\)(có 9 thừa số, mỗi thừa số là âm nên kết quả là âm)
\(B=-\left(\frac{1.3}{2.2}.\frac{2.4}{3.3}...\frac{9.11}{10.10}\right)\)
\(B=-\left(\frac{1.2...9}{2.3...10}.\frac{3.4...11}{2.3...10}\right)\)
\(B=-\left(\frac{1}{10}.\frac{11}{2}\right)\)
\(B=-\frac{11}{20}\)
HM
16 tháng 12 2015
(1+[-3])+(5+[-7])+...+(97+[-99])+101
= (-2) +(-2)+..+(-2)+101
=(-2).25+101
=-50+101
=51
tick đấy
22 tháng 3 2023
\(M=1+\dfrac{1}{5}+\dfrac{3}{35}+...+\dfrac{3}{9999}\\ =\dfrac{3}{3}+\dfrac{3}{15}+\dfrac{3}{35}+...+\dfrac{3}{9999}\\ =\dfrac{3}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{99\cdot101}\right)\\ =\dfrac{3}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\\ =\dfrac{3}{2}\left(1-\dfrac{1}{101}\right)=\dfrac{3}{2}\cdot\dfrac{100}{101}=\dfrac{150}{101}\)
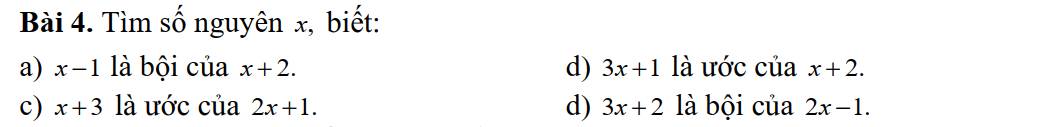
a) \(\left(x+3\right)\left(y-1\right)=3=\left(-3\right).\left(-1\right)=\left(-1\right).\left(-3\right)=3.1=1.3\)
Vậy ta tìm được các cặp giá trị \(\left(x;y\right)\) thỏa mãn đề bài:
\(\left(-6;0\right);\left(-4;-2\right);\left(-2;4\right);\left(0;2\right)\)
b) \(\left(2x+1\right)\left(y-2\right)=-12=\left(-12\right).1=\left(-6\right).2=\left(-4\right).3=\left(-3\right).4=\left(-2\right).6=\left(-1\right).12=1.\left(-12\right)=3.\left(-4\right)=4.\left(-3\right)=6.\left(-2\right)=12.\left(-1\right)\)
Vậy ta tìm được các cặp giá trị \(\left(x;y\right)\) thỏa mãn yêu cầu:
\(\left(-3;4\right);\left(-2;6\right);\left(-1;14\right);\left(0;-10\right);\left(1;-2\right)\)