Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 3:
a: Trên tia Ox, ta có: OA<OB
nên điểm A nằm giữa hai điểm O và B
=>OA+AB=OB
hay AB=2(cm)
b: Ta có: A nằm giữa hai điểm O và B
mà OA=AB
nên A là trung điểm của OB
c: Trên đoạn BO, ta có: BC<BO
nên điểm C nằm giữa hai điểm O và B
=>OC+CB=OB
hay OC=3cm
Trên tia Ox, ta có: OA<OC
nên điểm A nằm giữa hai điểm O và C
=>OA+AC=OC
hay AC=1cm

số học sinh xếp loại văn hóa giỏi là
50:10x3=15(h/sinh)
số học sinh còn lại là
50-15=35(h/sinh)
số học sinh loại khá là
35:8x3=

Đặt A=\(\dfrac{1}{11}\)+\(\dfrac{1}{12}\)+\(\dfrac{1}{13}\)+...\(\dfrac{1}{69}\)+\(\dfrac{1}{70}\)
=(\(\dfrac{1}{11}\)+\(\dfrac{1}{12}\)+\(\dfrac{1}{13}\)+...\(\dfrac{1}{19}\)+\(\dfrac{1}{20}\))+(\(\dfrac{1}{21}\)+\(\dfrac{1}{22}\)+\(\dfrac{1}{23}\)+...+\(\dfrac{1}{29}\)+\(\dfrac{1}{30}\))+(\(\dfrac{1}{31}\)+\(\dfrac{1}{32}\)+\(\dfrac{1}{33}\)+...+\(\dfrac{1}{59}\)+\(\dfrac{1}{60}\))+...+\(\dfrac{1}{70}\)
Nhận xét:
\(\dfrac{1}{11}\)+\(\dfrac{1}{12}\)+\(\dfrac{1}{13}\)+...+\(\dfrac{1}{19}\)+\(\dfrac{1}{20}\)>\(\dfrac{1}{20}\)+\(\dfrac{1}{20}\)+...+\(\dfrac{1}{20}\)=\(\dfrac{10}{20}\)=\(\dfrac{1}{2}\)
\(\dfrac{1}{21}\)+\(\dfrac{1}{22}\)+\(\dfrac{1}{23}\)+...+\(\dfrac{1}{29}\)+\(\dfrac{1}{30}\)>\(\dfrac{1}{30}\)+\(\dfrac{1}{30}\)+...+\(\dfrac{1}{30}\)=\(\dfrac{10}{30}\)=\(\dfrac{1}{3}\)
\(\dfrac{1}{31}\)+\(\dfrac{1}{32}\)+\(\dfrac{1}{33}\)+...+\(\dfrac{1}{59}\)+\(\dfrac{1}{60}\)>\(\dfrac{1}{60}\)+\(\dfrac{1}{60}\)+...+\(\dfrac{1}{60}\)=\(\dfrac{30}{60}\)=\(\dfrac{1}{2}\)
=>A>\(\dfrac{1}{2}\)+\(\dfrac{1}{3}\)+\(\dfrac{1}{2}\)+\(\dfrac{1}{61}\)+...+\(\dfrac{1}{69}\)+\(\dfrac{1}{70}\)>\(\dfrac{1}{2}\)+\(\dfrac{1}{3}\)+\(\dfrac{1}{2}\)=\(\dfrac{4}{3}\)
=>A>\(\dfrac{4}{3}\)
Vậy: \(\dfrac{1}{11}\)+\(\dfrac{1}{12}\)+\(\dfrac{1}{13}\)+...+\(\dfrac{1}{69}\)+\(\dfrac{1}{70}\)>\(\dfrac{4}{3}\) (ĐPCM)
Thấy đúng cho 1 tick và 1 follow nha!
Chúc bạn học tốt!

\(=\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{50}+\dfrac{1}{51}-\dfrac{102}{51\cdot52}\)
\(=\dfrac{1}{2}+\dfrac{1}{51}-\dfrac{102}{51\cdot52}\)
\(=\dfrac{1}{2}+\dfrac{52-102}{51\cdot52}=\dfrac{1}{2}+\dfrac{-50}{51\cdot52}=\dfrac{319}{663}\)


\(\dfrac{1}{2^2}>\dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
\(\dfrac{1}{3^2}>\dfrac{1}{3\cdot4}=\dfrac{1}{3}-\dfrac{1}{4}\)
...
\(\dfrac{1}{100^2}>\dfrac{1}{100\cdot101}=\dfrac{1}{100}-\dfrac{1}{101}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}>\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{100}-\dfrac{1}{101}=\dfrac{1}{2}-\dfrac{1}{101}=\dfrac{99}{202}\)
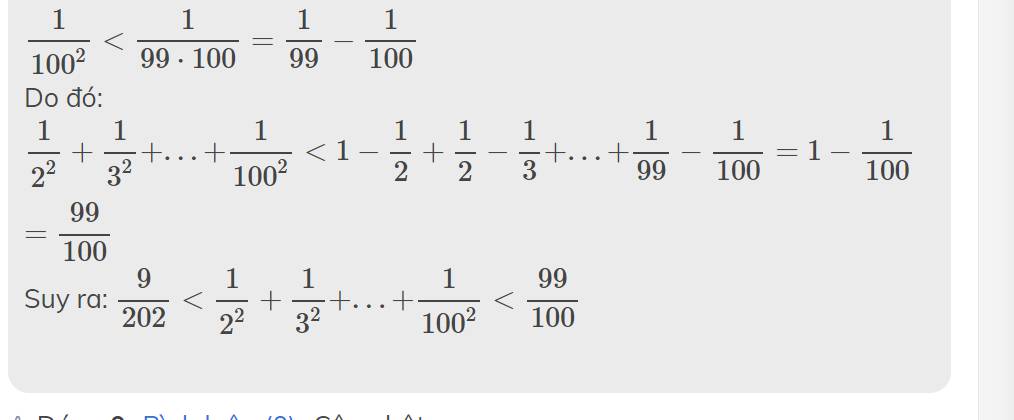
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{100^2}< \dfrac{1}{99\cdot100}=\dfrac{1}{99}-\dfrac{1}{100}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}=1-\dfrac{1}{100}=\dfrac{99}{100}\)
Suy ra: \(\dfrac{9}{202}< \dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< \dfrac{99}{100}\)


Có khi vậy,bn tìm hộ mk bài đó rùi lm cho mk nha,cảm ơn nhiều
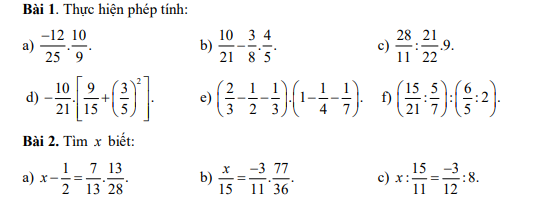
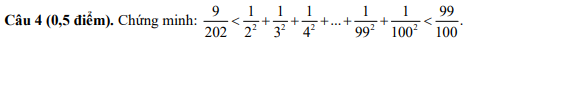



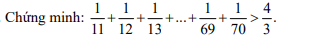
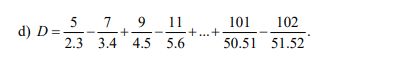

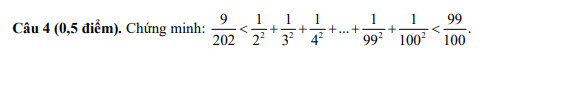
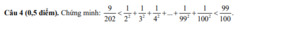
Bài 2:
a: \(x-\dfrac{1}{2}=\dfrac{7}{13}\cdot\dfrac{13}{28}\)
=>\(x-\dfrac{1}{2}=\dfrac{7}{28}=\dfrac{1}{4}\)
=>\(x=\dfrac{1}{4}+\dfrac{1}{2}=\dfrac{3}{4}\)
b: \(\dfrac{x}{15}=\dfrac{-3}{11}\cdot\dfrac{77}{36}\)
=>\(\dfrac{x}{15}=\dfrac{-3}{36}\cdot\dfrac{77}{11}=7\cdot\dfrac{-1}{12}=-\dfrac{7}{12}\)
=>\(x=-\dfrac{7}{12}\cdot15=-\dfrac{105}{12}=-\dfrac{35}{4}\)
c: \(x:\dfrac{15}{11}=\dfrac{-3}{12}:8\)
=>\(x:\dfrac{15}{11}=-\dfrac{1}{4}:8=-\dfrac{1}{32}\)
=>\(x=-\dfrac{1}{32}\cdot\dfrac{15}{11}=\dfrac{-15}{352}\)
Bài 1:
a: \(\dfrac{-12}{25}\cdot\dfrac{10}{9}=\dfrac{-12}{9}\cdot\dfrac{10}{25}=\dfrac{-4}{3}\cdot\dfrac{2}{5}=\dfrac{-8}{15}\)
b: \(\dfrac{10}{21}-\dfrac{3}{8}\cdot\dfrac{4}{5}\)
\(=\dfrac{10}{21}-\dfrac{12}{40}\)
\(=\dfrac{10}{21}-\dfrac{3}{10}=\dfrac{100-63}{210}=\dfrac{37}{210}\)
c: \(\dfrac{28}{11}:\dfrac{21}{22}\cdot9=\dfrac{28}{11}\cdot\dfrac{22}{21}\cdot9\)
\(=\dfrac{28}{21}\cdot\dfrac{22}{11}\cdot9=\dfrac{4}{3}\cdot2\cdot9=\dfrac{4}{3}\cdot18=24\)
d: \(-\dfrac{10}{21}\cdot\left[\dfrac{9}{15}+\left(\dfrac{3}{5}\right)^2\right]\)
\(=\dfrac{-10}{21}\cdot\left[\dfrac{3}{5}+\dfrac{9}{25}\right]\)
\(=\dfrac{-10}{21}\cdot\dfrac{15+9}{25}\)
\(=\dfrac{-10}{25}\cdot\dfrac{24}{21}=\dfrac{-2}{5}\cdot\dfrac{8}{7}=\dfrac{-16}{35}\)
e: \(\left(\dfrac{2}{3}-\dfrac{1}{2}-\dfrac{1}{3}\right)\cdot\left(1-\dfrac{1}{4}-\dfrac{1}{7}\right)\)
\(=\left(\dfrac{1}{3}-\dfrac{1}{2}\right)\cdot\dfrac{28-7-4}{28}\)
\(=\dfrac{-1}{6}\cdot\dfrac{17}{28}=\dfrac{-17}{168}\)
f: \(\left(\dfrac{15}{21}:\dfrac{5}{7}\right):\left(\dfrac{6}{5}:2\right)\)
\(=\left(\dfrac{5}{7}\cdot\dfrac{7}{5}\right):\left(\dfrac{6}{5\cdot2}\right)\)
\(=1:\dfrac{6}{10}=\dfrac{10}{6}=\dfrac{5}{3}\)