
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nếu đề bài cho vô hạn dấu căn thì ta làm như sau :
Nhận xét : A > 0
Ta có : \(A=\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{...}}}}}\)
\(\Rightarrow A^2=2\sqrt{2\sqrt{2\sqrt{2\sqrt{.....}}}}=2A\)
\(\Rightarrow A^2-2A=0\Rightarrow A\left(A-2\right)=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}A=0\left(\text{loại}\right)\\A=2\left(\text{nhận}\right)\end{array}\right.\)
Vậy A = 2

19. 3x2-4x+1
= 3x2-3x-x+1
= (3x2-3x)-(x-1)
= 3x(x-1)-(x-1)
= (3x-1)(x-1)
20.3x2+4x-7
= 3x2+3x-7x-7
= (3x2+3x)-(7x+7)
= 3x(x+1)-7(x-1)
= (3x-7)(x-1)
21.3x2+7x-6
= 3x2+9x-2x-6
= (3x2+9x)-(2x+6)
= 3x(x+3)-2(x+3)
= (3x-2)(x+3)
22.3x2+3x-6
= 3x2+6x-3x-6
=(3x2+6x)-(3x+6)
= 3x(x+2)-3(x+2)
=(3x-3)(x+2)
= 3(x-1)(x+2)
23. 3x2-3x-6
=(3x2-6x)+(3x-6)
=3x(x-2)+3(x-2)
=(3x+3)(x-2)
= 3(x+1)(x-2)
24.6x2-13x+6
= 6x2-9x-4x+6
= (6x2-9x)-(4x-6)
=3x(2x-3)-2(2x-3)
=(3x-2)(2x-3)
25.6x2+13x+6
= 6x2+9x+4x+6
= (6x2+9x)+(4x+6)
=3x(2x+3)+2(2x+3)
=(3x+2)(2x+3)
26. 6x2+15x+6
= (6x2+12x)+(3x+6)
= 6x(x+2)+3(x+2)
=(6x+3)(x+2)
=3(2x+1)(x+2)
27. 6x2-15x+6
= (6x2-12x)-(3x-6)
= 6x(x-2)-3(x-2)
=(6x-3)(x-2)
=3(2x-1)(x-2)
28. 6x2+20x+6
= (6x2+18x)+(2x+6)
= 6x(x+3)+2(x+3)
= (6x+2)(x+3)
= 2(3x+1)(x+3)
29.6x2-20x+6
= (6x2-18x)-(2x-6)
= 6x(x-3)+2(x-3)
= (6x-2)(x-3)
= 2(3x-1)(x-3)
30.6x2+12x+6
= (6x2+6x)+(6x+6)
= 6x(x+1)+6(x+1)
= (6x+6)(x+1)
= 6(x+1)(x+1)
= 6(x+1)2

(a+b)3+(c-a)3-(b+c)3=(b+c)((a+b)2-(a+b)(c-a)+(a-c)2)-(b+c)3=(b+c)(a2+b2+2ab+a2-ac-bc+ab+a2-2ac+c2-b2-c2-2bc)=(b+c)(3a2+3ab-3ac-3bc)=3(b+c)(a-c)(a+b)


\(A=x-x^2=-\left(x^2-x\right)=-\left(x^2-2\cdot\frac{1}{2}\cdot x+\frac{1}{4}-\frac{1}{4}\right)=-\left(x-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\)

1)\(6x-x^2=x\left(6-x\right)\)
2)\(5x^2z-15xyz+30xz^2=5x\left(xz-3y+6z\right)\)
3)\(x^3-6x^2+9x=x\left(x^2-6x+9\right)=x\left(x-3\right)^2\)

\(\dfrac{x+2}{x-2}-\dfrac{2}{x^2-2x}=\dfrac{1}{x}\left(đk:x\ne0,x\ne2\right)\)
\(\Leftrightarrow\dfrac{\left(x+2\right)x-2}{x\left(x-2\right)}=\dfrac{x^2-2x}{x\left(x-2\right)}\)
\(\Leftrightarrow x^2+2x-2=x^2-2x\)
\(\Leftrightarrow4x=2\Leftrightarrow x=\dfrac{1}{2}\)
Cho mình sửa lại nhé:
\(\dfrac{x+2}{x-2}-\dfrac{2}{x^2-2x}=\dfrac{1}{x}\left(đk:x\ne0,x\ne2\right)\)
\(\Leftrightarrow\dfrac{\left(x+2\right)x-2}{x\left(x-2\right)}=\dfrac{x-2}{x\left(x-2\right)}\)
\(\Leftrightarrow x^2+2x-2=x-2\)
\(\Leftrightarrow x^2+x=0\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)

Bài 1:
\(\Leftrightarrow\left[{}\begin{matrix}y=0\\y=3\end{matrix}\right.\)
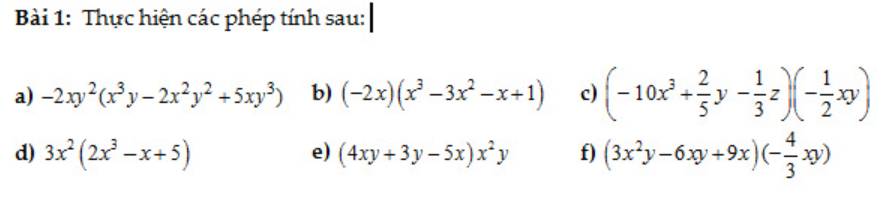


a) \(-2xy^2\left(x^3y-2x^2y^2-5xy^3\right)\)
\(=-2x^4y^3+4x^3y^4+10x^2y^5\)
b) \(\left(-2x\right)\left(x^3-3x^2-x+1\right)\)
\(=-2x^4+6x^3+2x^2-2x\)
c) \(\left(-10x^3-\dfrac{2}{5}y-\dfrac{1}{3}z\right)\left(-\dfrac{1}{2}xy\right)\)
\(=5x^4y+\dfrac{1}{5}xy^2+\dfrac{1}{6}xyz\)
d) \(3x^2\left(2x^3-x+5\right)\)
\(=6x^5-3x^3+15x^2\)
e) \(\left(4xy+3y-5x\right)x^2y\)
\(=4x^3y^2+3x^2y^2-5x^3y\)
f) \(\left(3x^2y-6xy+9x\right)\left(-\dfrac{4}{3}xy\right)\)
\(=-4x^3y^2+8x^2y^2-12x^2y\)
`@` `\text {Ans}`
`\downarrow`
`a)`
\(-2xy^2(x^3y-2x^2y^2+5xy^3)\)
`= (-2xy^2)(x^3y) + (-2xy^2)(-2x^2y^2)+(-2xy^2)(5xy^3)`
`=`\(-2x^4y^3+4x^3y^4-10x^2y^5\)
`b)`
\((-2x)(x^3-3x^2-x+1)\)
`= (-2x)(x^3) + (-2x)(-3x^2) + (-2x)(-x) + (-2x)`
`= -2x^4 + 6x^3 + 2x^2 - 2x`
`c)`
\(\left(-10x^3+\dfrac{2}{5}y-\dfrac{1}{3}z\right)\left(-\dfrac{1}{2}xy\right)\)
`=`\(-10x^3\left(-\dfrac{1}{2}xy\right)+\dfrac{2}{5}y\left(-\dfrac{1}{2}xy\right)-\dfrac{1}{3}z\left(-\dfrac{1}{2}xy\right)\)
`=`\(5x^4y-\dfrac{1}{5}xy^2+\dfrac{1}{6}xyz\)
`d)`
\(3x^2(2x^3-x+5)\)
`= 3x^2*2x^3 + 3x^2*(-x) + 3x^2*5`
`= 6x^5 - 3x^3 + 15x^2`
`e)`
\((4xy+3y-5x)x^2y\)
`=`\(4xy\cdot x^2y+3y\cdot x^2y-5x\cdot x^2y\)
`=`\(4x^3y^2+3x^2y^2-5x^3y\)
`f)`
\(\left(3x^2y-6xy+9x\right)\left(-\dfrac{4}{3}xy\right)\)
`=`\(3x^2y\cdot\left(-\dfrac{4}{3}xy\right)-6xy\cdot\left(-\dfrac{4}{3}xy\right)+9x\left(-\dfrac{4}{3}xy\right)\)
`=`\(-4x^3y^2+8x^2y^2-12x^2y\)
`\text {#KaizuulvG}`