
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
\(=\left(\dfrac{x}{x+3}-\dfrac{x^2+9}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{3x+1}{x\left(x-3\right)}-\dfrac{1}{x}\right)\)
\(=\left(\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{x^2+9}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{3x+1}{x\left(x-3\right)}-\dfrac{x-3}{x\left(x-3\right)}\right)\)
\(=\left(\dfrac{x^2-3x-x^2-9}{\left(x+3\right)\left(x-3\right)}\right):\left(\dfrac{3x+1-x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{-3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}:\dfrac{2x+4}{x\left(x-3\right)}\)
\(=\dfrac{-3}{\left(x-3\right)}\cdot\dfrac{x\left(x-3\right)}{2x+4}\\ =\dfrac{-3x}{2x+4}\)
b)
với `x=-1/2` (tmđk) ta có
\(\dfrac{-3\cdot\left(\dfrac{-1}{2}\right)}{2\cdot\left(-\dfrac{1}{2}\right)+4}=\dfrac{1}{2}\)
c)
để P=x thì
\(\dfrac{-3x}{2x+4}=x\)
\(=>-3x=\left(2x+4\right)\cdot x\)
\(-3x=2x^2+4x\)
\(2x^2+4x+3x=0\)
\(2x^2+7x=0\)
\(x\left(2x+7\right)=0\)
\(=>\left[{}\begin{matrix}x=0\\2x+7=0\end{matrix}\right.=>\left[{}\begin{matrix}x=0\left(loại\right)\\x=-\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)
d)
mik ko bt lm=)

\(15x^2y^5-10x^3y^4=5x^2y^4\left(3y-2x\right)\)
\(4x\left(x-2y\right)+7\left(2y-x\right)=4x\left(x-2y\right)-7\left(x-2y\right)=\left(x-2y\right)\left(4x-7\right)\)
\(5x^3+20x^2y+20xy^2=5x\left(x^2+4xy+4y^2\right)=5x\left(x+2y\right)^2\)
\(x^2-4y^2-2x+4y=\left(x-2y\right)\left(x+2y\right)-2\left(x-2y\right)=\left(x-2y\right)\left(x+2y-2\right)\)

a, \(\dfrac{2^3-x^3}{x\left(x^2+2x+4\right)}\) = \(\dfrac{\left(2-x\right)\left(x^2+2x+4\right)}{x\left(x^2+2x+4\right)}\) = \(\dfrac{2-x}{x}\)=\(\dfrac{x-2}{-x}\)(đpcm)
b, \(\dfrac{-3x\left(x-y\right)}{y^2-x^2}\) (\(x\) \(\ne\) \(\pm\) y)
= \(\dfrac{-3x\left(x-y\right)}{\left(y-x\right)\left(y+x\right)}\)
= \(\dfrac{3x\left(y-x\right)}{\left(y-x\right)\left(y+x\right)}\)
= \(\dfrac{3x}{x+y}\) (đpcm)

a: Thay x=-4 vào B, ta được:
\(B=\dfrac{1-2\cdot\left(-4\right)}{2-\left(-4\right)}=\dfrac{1+8}{2+4}=\dfrac{9}{6}=\dfrac{3}{2}\)

4: \(D=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
\(A=\left(x^2-6x+9\right)-7=\left(x-3\right)^2-7\ge7\\ A_{min}=7\Leftrightarrow x=3\\ B=\left(9x^2+6x+1\right)-4=\left(3x+1\right)^2-4\ge-4\\ B_{min}=-4\Leftrightarrow x=-\dfrac{1}{3}\\ C=\left(x^2-2\cdot\dfrac{5}{2}x+\dfrac{25}{4}\right)-\dfrac{9}{4}=\left(x-\dfrac{5}{2}\right)^2-\dfrac{9}{4}\ge-\dfrac{9}{4}\\ C_{min}=-\dfrac{9}{4}\Leftrightarrow x=\dfrac{5}{2}\\ D=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ D_{min}=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
\(E=3\left(x^2+2\cdot\dfrac{1}{3}x+\dfrac{1}{9}\right)-\dfrac{4}{3}=3\left(x+\dfrac{1}{3}\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\\ E_{min}=-\dfrac{4}{3}\Leftrightarrow x=-\dfrac{1}{3}\\ F=x^2-2x+1+x^2-4x+4+2021\\ F=2\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{4031}{2}=2\left(x-\dfrac{3}{2}\right)^2+\dfrac{4031}{2}\ge\dfrac{4031}{2}\\ F_{min}=\dfrac{4031}{2}\Leftrightarrow x=\dfrac{3}{2}\)

Bài 2:
a: =>168x+20=6x-21
=>162x=-41
hay x=-41/162
b: \(\Leftrightarrow2\left(3x-8\right)=3\left(5-x\right)\)
=>6x-16=15-3x
=>9x=31
hay x=31/9
c: \(\Leftrightarrow4\left(x^2+8x-20\right)-\left(x+4\right)\left(x+10\right)=3\left(x^2+2x-8\right)\)
\(\Leftrightarrow4x^2+32x-80-x^2-14x-40-3x^2-6x+24=0\)
=>12x-96=0
hay x=8

\(=\dfrac{5(x+4)}{(x+4)(x-4)}+\dfrac{4(x-4)}{(x+4)(x-4)}-\dfrac{2x-24}{(x+4)(x-4)} \\=\dfrac{7x+28}{(x+4)(x-4)} \\=\dfrac{7(x+4)}{(x+4)(x-4)} \\=\dfrac{7}{x-4}\)
b: \(=\dfrac{5x+20+4x-16-2x+24}{\left(x-4\right)\left(x+4\right)}=\dfrac{7x+28}{\left(x-4\right)\left(x+4\right)}=\dfrac{7}{x-4}\)

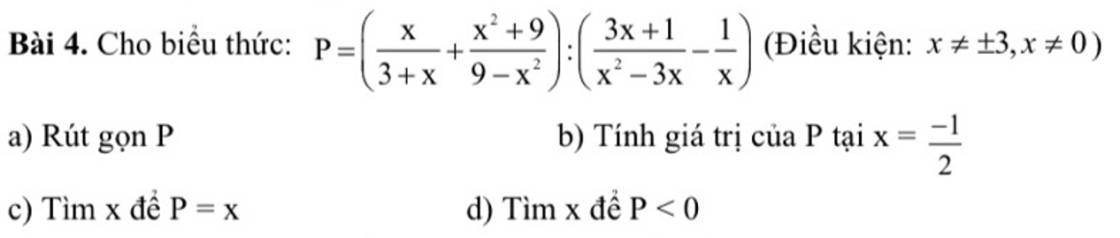
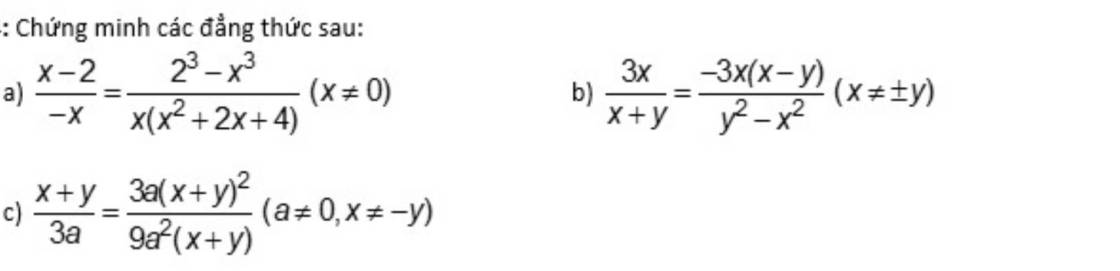


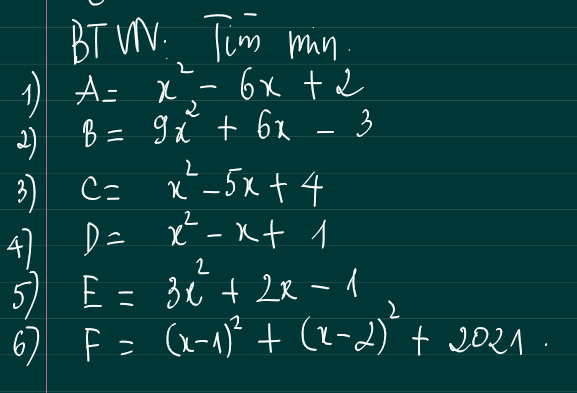

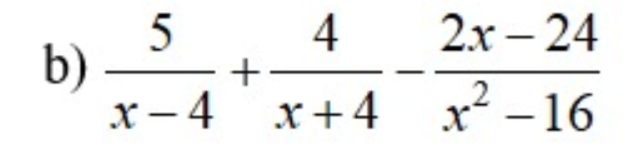


\(P=\frac{1}{1+a^2+b^2}+\frac{3}{2ab}=\left(\frac{1}{1+a^2+b^2}+\frac{\frac{1}{9}}{2ab}\right)+\frac{26}{18ab}\)
\(\ge\frac{\left(1+\frac{1}{3}\right)^2}{1+a^2+b^2+2ab}+\frac{26}{\frac{9\left(a+b\right)^2}{2}}\ge\frac{\frac{16}{9}}{2}+\frac{26}{\frac{9}{2}}=\frac{20}{3}\)