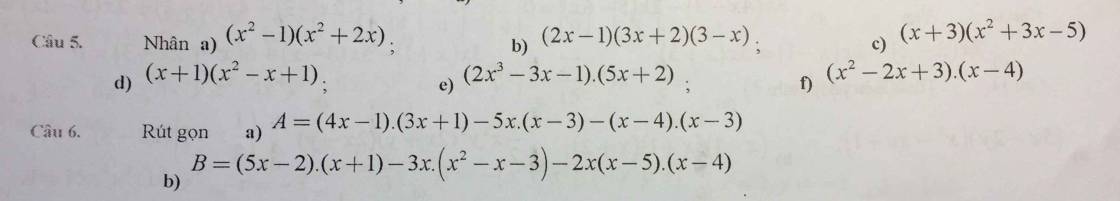AN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7N
Giúp mk câu 1 với mk cần gấp, cảm ơn mn rất nhiều
4
10 tháng 12 2021
đây là bài cũ bn ạ, bài này lâu r. ko kiểm tra đâu ạ
NL
2
3 tháng 10 2021
\(\left|3x+2\right|=\left|4x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+2=4x-3\\3x+2=3-4x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=-5\\7x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{1}{7}\end{matrix}\right.\)
3 tháng 10 2021
\(\left|2+3x\right|=\left|4x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2+3x=4x-3\\2+3x=3-4x\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{1}{7}\end{matrix}\right.\)
1 tháng 12 2019
<=>(x-4)(x+1)(x-4)<0
<=> (x-4)^2(x+1)<0 mà (x-4)^2>=0
<=> x+1<0<=> x<-1
1 tháng 12 2019
sr bn mình viết sai đề phải là\(\left(x-2\right)^2\left(x+1\right)\left(x-4\right)< 0\)
7N
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
3
24 tháng 10 2021
Bài 3:
1, Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{z-x}{3-6}=\dfrac{-21}{-3}=7\\ \Rightarrow\left\{{}\begin{matrix}x=42\\y=28\\z=21\end{matrix}\right.\)
2, Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{2x+3y-z}{6+15-7}=\dfrac{-14}{14}=-1\\ \Rightarrow\left\{{}\begin{matrix}x=-3\\y=-5\\z=-7\end{matrix}\right.\)
24 tháng 10 2021
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x+y+z}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}}=\dfrac{130}{\dfrac{13}{12}}=120\)
Do đó: x=60; y=40; z=30
J
10 tháng 7 2017
a) \(\left(2x-3\right)\left(\frac{3}{4}x+1\right)=0\)
<=>\(\hept{\begin{cases}2x-3=0\\\frac{3}{4}x+1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}2x=3\\\frac{3}{4}x=-1\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{3}{2}\\x=-\frac{3}{4}\end{cases}}}\)
b) \(\left(5x-1\right)\left(2x-\frac{1}{3}\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}5x-1=0\\2x-\frac{1}{3}=0\end{cases}\Leftrightarrow\hept{\begin{cases}5x=1\\2x=\frac{1}{3}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{1}{5}\\x=\frac{1}{6}\end{cases}}}\)
2 tháng 3 2023
Câu 6:
a: =12x^2+4x-3x-1-5x^2+15x-x^2+7x-12
=6x^2+23x-13
b: =5x^2+5x-2x-2-3x^3+3x^2+9x-2x(x^2-9x+20)
=-3x^3+8x^2+14x-2-2x^3+18x^2-40x
=-5x^3+26x^2-26x-2
10 tháng 9 2017
Giả sử 2 dường thẳng xx' và yy' cắt nhau tại O
Kẻ Ot là tia fg góc xOy
và Ot' là tia fg góc x'Oy'. Ta phải chứng minh Ot và Ot' cùng nằm trên 1 đường thẳng hay tOt'=180o
tOt'=tOx+xOt' (tia Ox nằm giữa 2 tia Ot,Ot')
mà tOx=x'Ot' (cùng =1/2 hai góc đối đỉnh)
nên tOt'=x'Ot'+t'Ox=xOx'=180o (tia Ot' nằm giữa 2 tia Ox,Ox')
vậy Ot và Ot'là 2 tia đối nhau
.
S
10 tháng 9 2017
a, Ta có: \(A=\left|x+2\right|+\left|9-x\right|\ge\left|X+2+9-x\right|=11\)
Dấu "=' xảy ra khi \(\left(x+2\right)\left(9-x\right)\ge0\Leftrightarrow-2\le x\le9\)
Vậy MinA = 11 khi -2 =< x =< 9
b, Vì \(\left(x-1\right)^2\ge0\Rightarrow-\left(x-1\right)^2\le0\Rightarrow B=\frac{3}{4}-\left(x-1\right)^2\le\frac{3}{4}\)
Dấu "=" xảy ra khi x = 1
Vậy MaxB = 3/4 khi x=1
10 tháng 9 2017
Ta có :\(A=\left|x+2\right|+\left|9-x\right|\ge\left|x+2+9-x\right|=11\)
Vậy \(A_{min}=11\) khi \(2\le x\le9\)