
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



`a(a+6)+10>0`
`<=>a^2+6a+10>0`
`<=>a^2+6a+9+1>0`
`<=>(a+3)^2+1>0` luôn đúng

cái này thì ko nhất thiết phải Cm nha bạn
Câu b kêu tìm x để B ko nhỏ hơn hoặc bằng A
Nghĩa là
\(\dfrac{4}{3-\sqrt{x}}>1\)
\(\Leftrightarrow\dfrac{4}{3-\sqrt{x}}-1>0\)
\(\Leftrightarrow\dfrac{4-\left(3-\sqrt{x}\right)}{3-\sqrt{x}}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{3-\sqrt{x}}>0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}+1>0\\3-\sqrt{x}>0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}+1< 0\left(VL\right)\\3-\sqrt{x}< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 3\)
\(\Leftrightarrow x< 9\)
Theo Đk ta có x≥0
Vậy 0≤x<9 thì B ko nhỏ hơn hoặc bằng A
\(\sqrt{x}\ge0\Leftrightarrow\sqrt{x}+1\ge1>0\)
Hiển nhiên nhé

Bài 1:
Nếu chị nhớ không nhầm thì phải là \(\left[\begin{matrix} \frac{1}{2}\leq x< 2\\ 0< x<\frac{1}{2}\end{matrix}\right.\)
Tức là $x$ nhận các khoảng giá trị sau:
\(0< x< \frac{1}{2}\); \(x=\frac{1}{2}\); \(\frac{1}{2}< x< 2\)
Vậy có nghĩa $0< x< 2$ (rất dễ hiểu mà????)
Bài 2:
Ngoặc nhọn dùng khi muốn biểu thị hai/ nhiều phương trình/ bất phương trình đồng thời xảy ra cùng một lúc
Ngoặc vuông dùng khi muốn biểu thị cái này hoặc cái kia xảy ra.
Bài trên phải dùng ngoặc vuông là sao em? Ngoặc nhọn thường xuất hiện trong bài toán giải hệ phương trình, bất phương trình. Còn ngoặc vuông thì thường dùng kết luận nghiệm của pt/ bpt.
Kết hợp điều kiện thì dùng ngoặc nhọn. Ví dụ $\sqrt{x+1}+\sqrt{2-x}$ thì việc $x+1\geq 0$ và $2-x\geq 0$ phải đồng thời xảy ra cùng lúc.

Bởi vì ta có tính chất:
`a>=b>0=>1/a<=1/b`
GTLN bởi vì có dấu `<=`

Vì xe thứ nhất đi trước xe thứ hai 20ph ấy bạn mà cùng đến tp B cùng một lúc,bởi thế nên thgian oto thứ nhất-thgian oto thứ hai =1/3(ở đây là 20ph)
Gọi vận tốc của hai xe ô tô thứ nhất là: \(x\)(km/h) và thứ 2 là \(y\)(km/h) (x,y >0)
\(\Rightarrow y-x=6\)
\(\Rightarrow y=x+6\) (km/h)
\(\Rightarrow\)Thời gian xe thứ nhất và xe thứ hai là\(\dfrac{144}{x};\dfrac{144}{y}\)\(=\dfrac{144}{x+6}\)(h)
Vì xe thứ hai đi sau xe thứ nhất 20p\(=\dfrac{1}{3}giờ\) và đến B cùng lúc nên thời gian đi hết AB của xe thứ nhất nhiều hơn \(\dfrac{1}{3}giờ\)
⇒\(\dfrac{144}{x}-\dfrac{144}{x+6}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{144\left(x+6\right)-144x}{x\left(x+6\right)}=\dfrac{1}{3}\)
\(\Rightarrow x^2+6x=3.144.6\)
\(\Rightarrow x^2+6x-2592=0\)
\(\Rightarrow\left(x-48\right)\left(x+54\right)=0\)
\(x=48\left(\dfrac{km}{h}\right)\) (do x>0)
Vậy vận tốc của hai xe là 48km/h và 54km/h

\(2\sqrt{6}+\sqrt{3}+4\sqrt{2}+3\)
\(=\left(\sqrt{2}+\sqrt{3}+\sqrt{6}\right)+\left(3\sqrt{2}+3+\sqrt{6}\right)\)
\(=\left(\sqrt{2}+\sqrt{3}+\sqrt{6}\right)+\left(\sqrt{18}+\sqrt{9}+\sqrt{6}\right)\)
\(=\left(\sqrt{2}+\sqrt{3}+\sqrt{6}\right)+\left(\sqrt{3.6}+\sqrt{3.3}+\sqrt{3.2}\right)\)
\(=\left(\sqrt{2}+\sqrt{3}+\sqrt{6}\right)+\sqrt{3}\left(\sqrt{2}+\sqrt{3}+\sqrt{6}\right)\)


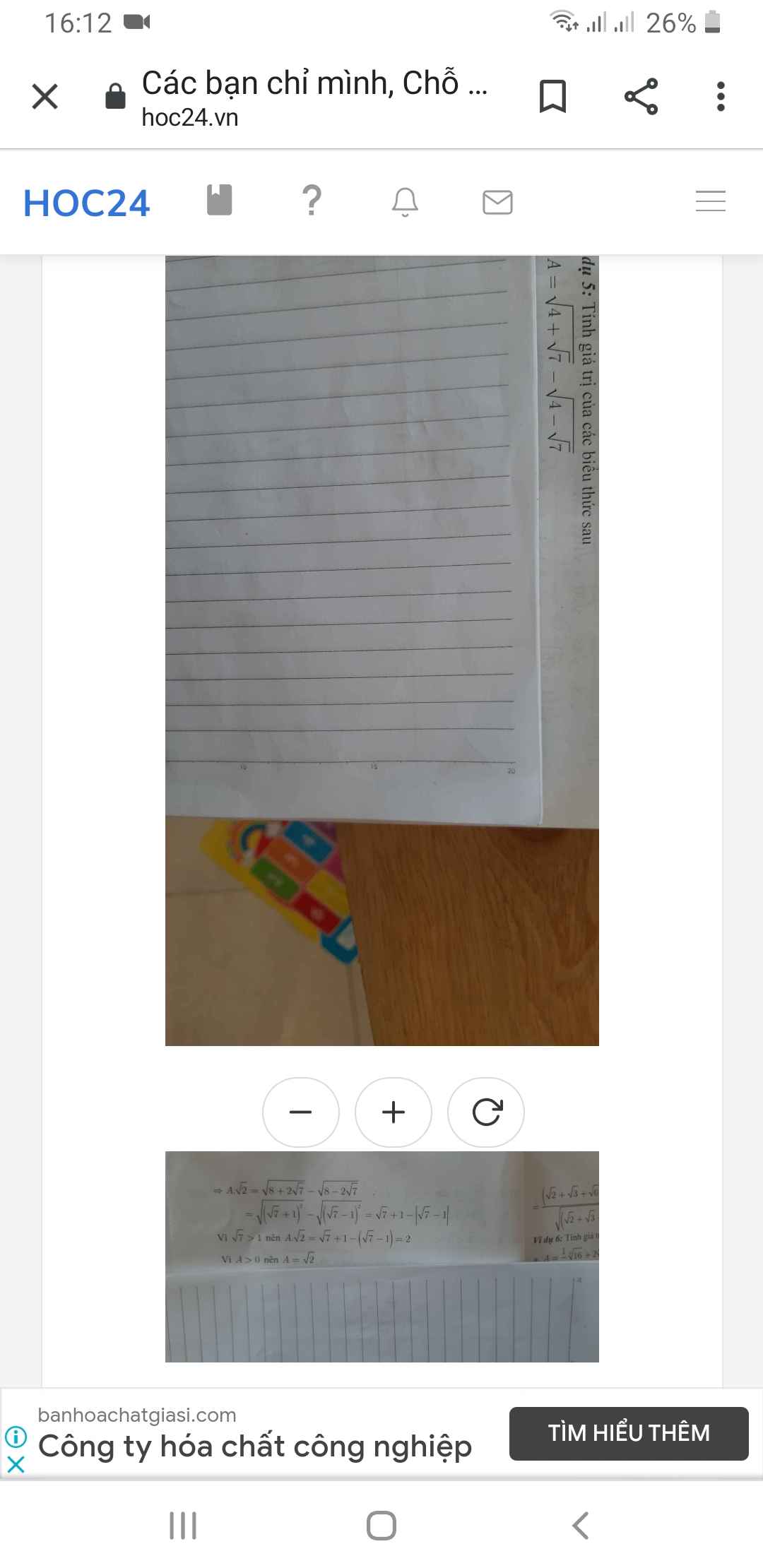





Do \(4+\sqrt{7}>4-\sqrt{7}\)
\(\Rightarrow\sqrt{4+\sqrt{7}}>\sqrt{4-\sqrt{7}}\)
\(\Rightarrow\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}>0\)
Hay \(A>0\)