Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì mỗi đơn thức là một đa thức nên ta có thể viết bất kỳ đơn thức nào ở câu này.
Ví dụ: P(x) = xy2 (Vì đơn thức cũng là một đa thức)
b) Có vô số đa thức không phải là đơn thức.
Ví dụ: 2x + 3y; x2 + 2y

Ba đơn thức có thể là `3/7x^2; 4x^2; -9x^2`.
So sánh: `-9 < 4<3/7`.

a: x là đơn thức một biến
b: A(x)=-x^2+2/3x-1
Đặt A(x)=0
=>-x^2+2/3x-1=0
=>x^2-2/3x+1=0
=>x^2-2/3x+1/9+8/9=0
=>(x-1/3)^2+8/9=0(vô lý)
c: B(-3)=(-3)^2+4*(-3)-5
=9-5-12
=4-12=-8

Nhóm 1: \({x^3} - \dfrac{1}{2}x; - 2x + 7y;x + 2y - z.\)
Nhóm 2: \( - 5{x^2}y;17{z^4}; - \dfrac{1}{5}{y^2}5;xy4{x^2}.\)
Nhóm 2 bao gồm những đơn thức vì chỉ gồm tích của số và các biến.

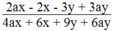 xác định khi 4ax + 6x + 9y + 6ay
≠
0
xác định khi 4ax + 6x + 9y + 6ay
≠
0
⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y) ≠ 0
Ta có: 2a + 3 ≠ 0 ⇒ a ≠ - 3/2 ; 2x + 3y ≠ 0 ⇒ x ≠ - 3/2 y
Điều kiện: x ≠ - 3/2 y và a ≠ - 3/2
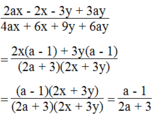
Vậy biểu thức không phụ thuộc vào x, y.

Ví dụ: phương trình (1) x - 1 = 3 có tập nghiệm S1 = {4}.
Nhân hai vế của phương trình (1) với x, ta được phương trình:
(x - 1)x = 3x (2)
⇔ (x - 1)x - 3x = 0
⇔ x(x - 4) = 0
Phương trình (2) có tập nghiệm là S2 = {0, 4}.
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.
3. Với điều kiện nào của a thì phương trình ax + b = 0 là một phương trình bậc nhất? (a và b là hai hằng số).

Biểu thức \({x^2} - 2x\) không là đơn thức một biến vì trong biểu thức có chứa phép trừ.
Ví dụ về đơn thức một biến:\({x^2};\dfrac{1}{2}x; - 3{x^3};....\)