Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Tiền lương cơ bản:
$26.200=5200$ (nghìn đồng)
Tiền lương tăng ca:
$10.3.\frac{200.1,5}{8}=1125$ (nghìn đồng)
Tổng tiền lương: $5200+1125=6235$ (nghìn đồng) hay $6235000$ đồng

Mức lương cơ bản người đó nhận đc trong 1 giờ: \(200000:8=25000\left(đồng\right)\)
Mỗi giờ tăng ca người đó được \(25000\cdot150\%=37500\left(đồng\right)\)
Tổng tiền người đó đc trong 1 tháng \(200000\cdot26+3\cdot10\cdot37500=6325000\left(đồng\right)\)

a: Khi x=9 thì y=208-0,7*9=201,7
b: Vì a=-0,7<0 nên hàm số nghịch biến trên R
=>Khi x tăng thì y giảm
=>Khi độ tuổi càng cao thì nhịp tim tối đa được khuyến cáo càng giảm xuống

biên luân ban tu lm nhe mk chi ghi hê pt ra thôi \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\\\frac{1}{x}-\frac{1}{y}=\frac{1}{2}\end{cases}}\) ban tu giai nhe

Gọi người 1 , 2 làm trong k , t ngày thì xong công việc ( k,t>0 )
Ta có hệ pt \(\int^{\frac{2}{k}+\frac{5}{t}=\frac{1}{2}}_{\frac{3}{k}+\frac{3}{t}=1-\frac{1}{20}}\)

Đổi : \(\frac{12}{5}\)= \(2,4\)giờ
Người thứ hai làm xong trong thời gian là :
( 2,4 - 2 ) : 2 = 0,2 giờ hay 12 phút
Người thứ nhất làm xong trong thời gian là :
2,4 - 0,2 = 2,2 giờ hay 2 giờ 12 phút
Đ/s : người thứ nhất : 2 giờ 12 phút
người thứ hai : 12 phút .

Bài 1 :
Gọi giá tiền của một chiếc ti vi loại A là x (triệu đồng) và giá tiền của một chiếc máy giặt loại B là y (triệu đồng)
Do tổng giá của 2 mặt hàng là 25,425,4 triệu nên ta có
\(x+y=25,4\)
Giá tiền của ti vi loại A và máy giặt loại B sau khi giảm giá là 0,6x(triệu đồng) và 0,75y(triệu đồng).
Do khi đó tổng giá tiền là 16,77 triệu đồng nên ta có
\(0,6x+0,75y=16,77\)
Vậy ta có hệ
\(\hept{\begin{cases}x+y=25,4\\0,6x+0,75y=16,77\end{cases}}\)
Giải ra ta có
x=15,2 ; y=10,2
Vậy giá niêm yết của ti vi loại A là 15,2 triệu đồng.
Bài 2 :
Gọi quãng đường AB là x(km) và khoảng thời gian sau khi xe tải xuất phát là y(h).
Vậy thời gian đi của xe tải là \(\frac{x}{40}\left(h\right)\)thời gian đi dự kiến của xe 45 chỗ là \(\frac{x}{50}\left(h\right)\)
Do đó ta có
\(\frac{x}{40}=\frac{x}{50}+y\)
\(\Leftrightarrow\frac{x}{200}=y\)
\(\Leftrightarrow x=200y\)
Thời gian đi thực tế của xe 45 chỗ là
\(\frac{x}{2}:50+\frac{x}{2}:60=\frac{x}{100}+\frac{x}{120}=\frac{11x}{600}\left(h\right)\)
Mà khi đó xe 45 chỗ đến B trc xe tải \(41'=\frac{41}{60}\left(h\right)\) nên ta có
\(\frac{x}{40}=\frac{11x}{600}+y+\frac{41}{60}\)
\(\Leftrightarrow\frac{x}{150}=y+\frac{41}{60}\)
\(\Leftrightarrow2x=300y+205\)
\(\Leftrightarrow2x-300y=205\)
Vậy ta có hệ
\(\hept{\begin{cases}x=200y\\2x-300y=205\end{cases}}\)
Sử dụng phương pháp thế giải ra \(x=410\)
Vậy quãng đường AB dài 410(km).
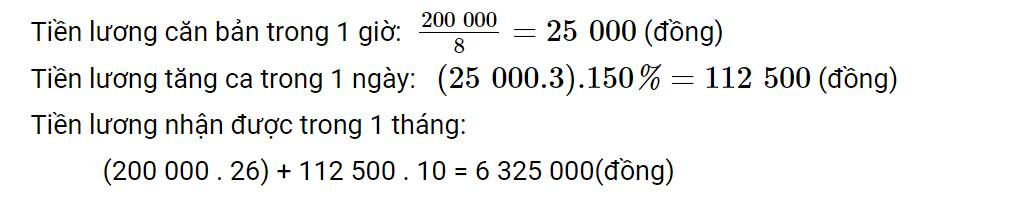
 thế này ai mà trả lời được.
thế này ai mà trả lời được.
a) Nhiệt độ t (⁰C) tuần tới tại Tokyo là:
t > -5
b) Gọi x (tuổi) là tuổi của người điều khiển xe máy điện. Ta có bất đẳng thức:
x ≥ 16
c) Gọi z (đồng) là mức lương tối thiểu trong một giờ làm việc của người lao động. Ta có bất đẳng thức:
z ≥ 20000
d) y là số dương nên ta có bất đẳng thức:
y > 0
a, t>5
b,x≥16
c,mức lương tối thiểu≤20 000đ
d, y>0